
分析 (1)设生产一辆B型单车的成本为x元,则生产一辆A型单车的成本为(x+100)元,根据数量=总价÷单价结合60万元全部生产A型单车的数量比全部生产B型单车的数量少300辆,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设生产A型单车m辆,则生产B型单车(10000-m)辆,根据总成本=单辆成本×生产数量结合总成本不超过471万元,即可得出关于m的一元一次不等式,解之即可得出结论;
(3)设该厂获得的总利润为y元,根据总利润=单辆利润×生产辆数,即可得出y关于m的函数关系式,根据一次函数的性质结合m的取值范围,即可解决最值问题.
解答 解:(1)设生产一辆B型单车的成本为x元,则生产一辆A型单车的成本为(x+100)元,
根据题意得:$\frac{600000}{x}$-$\frac{600000}{x+100}$=300,
解得:x=400或x=-500(不合题意,舍去),
经检验,x=400是原分式方程的解,
∴x+100=500.
答:生产一辆B型单车的成本为400元,生产一辆A型单车的成本为500元.
(2)设生产A型单车m辆,则生产B型单车(10000-m)辆,
根据题意得:500×(1-10%)m+400×(1+20%)(10000-m)≤4710000,
解得:m≥3000.
答:至少要生产3000辆A型单车.
(3)设该厂获得的总利润为y元,
根据题意得:y=150m+180(10000-m)=1800000-30m,
∵-30<0,
∴y值随m的增大而减小,
∴当m=3000时,y取最大值,此时y=1800000-30×3000=1710000.
答:生产3000辆A型单车、7000辆B型单车时,获得的利润最大,最大值为171万元.
点评 本题考查了一次函数的应用、分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)根据数量=总价÷单价列出关于x的分式方程:(2)根据总成本=单辆成本×生产数量结合总成本不超过471万元,列出关于m的一元一次不等式;(3)根据总利润=单辆利润×生产辆数,找出y关于m的函数关系式.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{12}{7}$≤t<-$\frac{8}{7}$ | B. | -$\frac{12}{7}$≤t<-$\frac{3}{2}$ | C. | -$\frac{3}{2}$≤t<-$\frac{4}{3}$ | D. | -$\frac{4}{3}$≤t<-$\frac{8}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知函数y=2+$\frac{4}{x}$.
已知函数y=2+$\frac{4}{x}$.| x | … | -8 | -4 | -3 | -2 | -1 | -$\frac{1}{2}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | 8 | … |
| y | … | $\frac{3}{2}$ | 1 | $\frac{2}{3}$ | 0 | -2 | -6 | 10 | 6 | 4 | $\frac{10}{3}$ | 3 | $\frac{5}{2}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
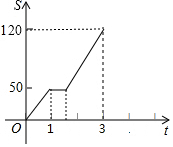 小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )
小敏驾驶汽车行驶1小时后,在服务区休息了一会儿,然后继续以原速度匀速行驶,其路程S(千米)与时间t(小时)的关系如图所示,则小敏在服务区休息的时间为( )| A. | 0.5小时 | B. | 0.6小时 | C. | 0.7小时 | D. | 0.8小时 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
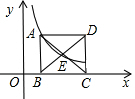 已知点(1,3)在函数y=$\frac{k}{x}$(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).
已知点(1,3)在函数y=$\frac{k}{x}$(x>0)的图象上,正方形ABCD的边BC在x轴上,点E是对角线AC、BD的交点,函数y=$\frac{k}{x}$(x>0)的图象又经过A、E两点,则点E的坐标为($\sqrt{6}$,$\frac{\sqrt{6}}{2}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com