练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    用因式分解法解方程：（1+3x）2=4（x-3）2．
    考点：解一元二次方程-因式分解法
    专题：计算题
    分析：方程移项后，利用因式分解法求出解即可．
    解答：解：方程移项得：（1+3x）2-4（x-3）2=0，
    分解因式得：[（1+3x）+2（x-3）][（1+3x）-2（x-3）]=0，
    可得5x-5=0或x+7=0，
    解得：x1=1，x2=-7．
    点评：此题考查了解一元二次方程-因式分解法，熟练掌握因式分解的方法是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

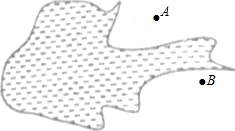    如图所示，某湖泊岸有A、B两棵大树，想在两棵大树间架一条电话线路．为了计算两棵大树能承受的压力，需测量出A、B之间的距离，但是A、B两点又不能直接到达，你能用已学过的知识和方法设计测量方案，求出A、B两点间的距离吗？并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知a2-2a+1=0，求a+
    1
    a
    与a2+
    1
    a2
    值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    x=2
     
    （填“是”或“不是”）方程3x+2=-
    1
    2
    x+9的解．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    当a=-3.4，b=-2
    2
    5
    时，（-a）-b=
     
    ，（-a）-（-b）=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    用代入法消去t，则方程组
    3y-2t-1=0
    2x+5t=0
    中x与y的关系为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （1）计算：（a+b+c）×（a2+b2+c2-ab-bc-ca）；
    （2）已知a+b+c=0．a，b，c均不为0，求
    a3+b3+c3
    abc
    的值．提示：由题1可得（a+b+c）×（a2+b2+c2-ab-bc-ac）=a3+b3+c3-3abc．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在一副三角板中，∠AOB=90°，∠COD=45°，将顶点O重合在一起，三角板ODC绕着点O顺时针旋转．
    （1）如图①，当OC与OB边重合时，∠AOD的度数是
     
    ；
    （2）当三角板ODC转到恰好使OB平分∠COD时（如图②），∠AOC的度数是
     
    ；
    （3）三角板ODC转到边OC、OD都在∠AOB的内部，作∠AOC的平分线OM，作∠BOD的平分线ON，如图③，那么，当三角板ODC转动时，∠MON的度数会变化吗？若不变，求这个角的度数；若有变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    用简便方法计算．
    （1）1232-124×122                 
    （2）42014×（-
    2
    3
    ）2013×（1
    1
    2
    ）2012×0.252012．

    查看答案和解析>>

    同步练习册答案