
分析 先根据根与系数的关系得到x1+x2=-2,x1x2=-10,再进行代数式变形,
(1)x12+x22=(x1+x2)2-2x1x2;
(2)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$;
(3)(x1-5)(x2-5)=x1x2-5(x1+x2)+25;
(4)|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$;
然后分别利用整体代入的方法计算即可.
解答 解:∵x1,x2是方程x2+2x-10=0的两个根,
∴x1+x2=-2,x1x2=-10,
(1)x12+x22=(x1+x2)2-2x1x2=24;
(2)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{1}{5}$;
(3)(x1-5)(x2-5)=x1x2-5(x1+x2)+25=25;
(4)|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=2$\sqrt{11}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABD和△ACE中,AB=AC,有下列三个等式:
如图,在△ABD和△ACE中,AB=AC,有下列三个等式:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
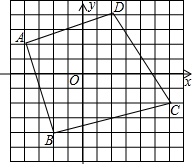 已知,如图,四边形ABCD的顶点坐标分别为A(-4,2),B(-2,-4),C(6,-2),D(2,4),试以O点为位似中心作四边形A′B′C′D′,使四边形ABCD与四边形A′B′C′D′的位似比为2:1(只画一种情况).
已知,如图,四边形ABCD的顶点坐标分别为A(-4,2),B(-2,-4),C(6,-2),D(2,4),试以O点为位似中心作四边形A′B′C′D′,使四边形ABCD与四边形A′B′C′D′的位似比为2:1(只画一种情况).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
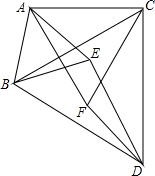 如图,以△ABC的各边为边,在BC的同一侧作等边三角形DBC,等边三角形ABE,等边三角形△ACF.
如图,以△ABC的各边为边,在BC的同一侧作等边三角形DBC,等边三角形ABE,等边三角形△ACF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com