
 如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠C=∠E=90°,AC=DE=12,BC=FE=16,点D是AB的中点,将△DEF绕点D旋转,DE、DF分别交BC于点G、H,使DG=GH,则重叠部分(△DGH)的面积为
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠C=∠E=90°,AC=DE=12,BC=FE=16,点D是AB的中点,将△DEF绕点D旋转,DE、DF分别交BC于点G、H,使DG=GH,则重叠部分(△DGH)的面积为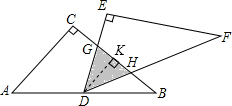 解:如图,过点D作DK⊥BC于K,
解:如图,过点D作DK⊥BC于K,| AC |
| HK |
| BC |
| DK |
| 1 |
| 2 |
| 1 |
| 2 |
| 12 |
| HK |
| 16 |
| 6 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 25 |
| 4 |
| 1 |
| 2 |
| 25 |
| 4 |
| 75 |
| 4 |
| 75 |
| 4 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
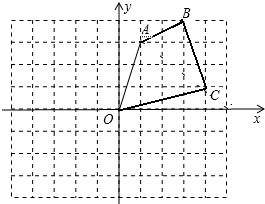 在如图所示的边长均为1的正方形的方格纸中,建立直角坐标系,四边形OABC的位置如图所示.请将此四边形的各个顶点的横坐标不变,纵坐标分别乘-1,得到一个新图形,画出新的图形,并求出此图形的面积.
在如图所示的边长均为1的正方形的方格纸中,建立直角坐标系,四边形OABC的位置如图所示.请将此四边形的各个顶点的横坐标不变,纵坐标分别乘-1,得到一个新图形,画出新的图形,并求出此图形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:
| ax+b |
查看答案和解析>>
科目:初中数学 来源: 题型:
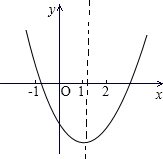 二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-b,则( )
二次函数y=ax2+bx+c的图象如图所示,若M=4a+2b+c,N=a-b+c,P=4a-b,则( )| A、M>0,N>0,P>0 |
| B、M<0,N>0,P>0 |
| C、M>0,N<0,P>0 |
| D、M<0,N>0,P<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:
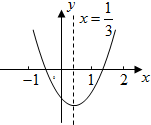 小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面信息:
小明从图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面信息:| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
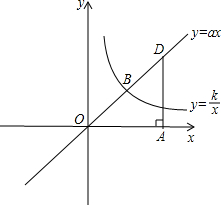 已知正比例函数y=ax与反比例函数y=
已知正比例函数y=ax与反比例函数y=| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com