
分析 首先计算乘方、开方,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
解答 解:$\sqrt{8}$+($\frac{1}{3}$)-1+|$\sqrt{2}-2$|-2cos45°
=2$\sqrt{2}$+3+2-$\sqrt{2}$-2×$\frac{\sqrt{2}}{2}$
=$\sqrt{2}$+5-$\sqrt{2}$
=5
点评 此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.


科目:初中数学 来源: 题型:解答题
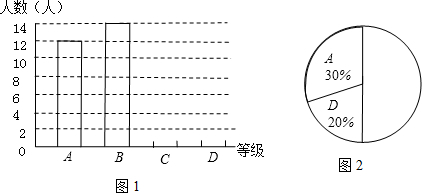
| 等级 | 一分钟跳 绳次数x | 人数 |
| A | x>180 | 12 |
| B | 150<x≤180 | 14 |
| C | 120<x≤150 | a |
| D | x≤120 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
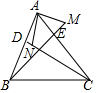 如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.
如图,△ABC中,CD、BE是边AB和AC上的高,点M在BE的延长线上,且BM=AC,点N在CD上,且AB=CN,则∠MAN的度数是90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
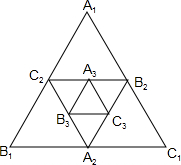 如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=$\frac{\sqrt{3}}{{4}^{20}}$.
如图,小强作出边长为1的第1个等边△A1B1C1,计算器面积为S1,然后分别取△A1B1C1三边的中点A2、B2、C1,作出第2个等边△A2B2C2,计算其面积为S2,用同样的方法,作出第3个等边△A3B3C3,计算其面积为S3,按此规律进行下去,…,由此可得,第20个等边△A20B20C20的面积S20=$\frac{\sqrt{3}}{{4}^{20}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
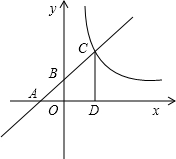 如图:已知一次函数y=kx+b(k≠0)的图象与x轴、y轴的交点分别为A、B两点.且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.
如图:已知一次函数y=kx+b(k≠0)的图象与x轴、y轴的交点分别为A、B两点.且与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,CD垂直于x轴,垂足为D,若OA=OB=OD=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com