
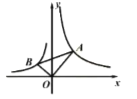
【题目】如图,将一块含![]() 的三角板(
的三角板(![]() )放置在坐标系中,直角顶点与原点
)放置在坐标系中,直角顶点与原点![]() 重合,另两个顶点
重合,另两个顶点![]() 、
、![]() 分别在反比例函数
分别在反比例函数![]() 和
和![]() 的图像上,
的图像上,![]() 的值为___________.
的值为___________.
 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
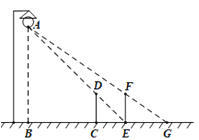
【题目】甲乙两位同学利用灯光下的影子来测量一路灯A的高度,如图,当甲走到点C处时,乙测得甲直立身高CD与其影子长CE正好相等,接着甲沿BC方向继续向前走,走到点E处时,甲直立身高EF的影子恰好是线段EG,并测得EG=2.5m.已知甲直立时的身高为1.75m,求路灯的高AB的长.(结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上。甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地。两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示。
(分钟)之间的函数关系如图所示。
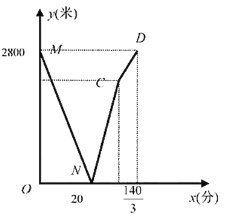
(1)当![]() ____________分钟时甲、乙两人相遇,乙的速度为__________米/分钟,点
____________分钟时甲、乙两人相遇,乙的速度为__________米/分钟,点![]() 的坐标为_____________;
的坐标为_____________;
(2)求出甲、乙两人相遇后![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)当乙到达距学校800米处时,求甲、乙两人之间的距离。
查看答案和解析>>
科目:初中数学 来源: 题型:
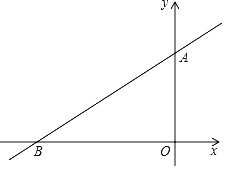
【题目】如图,在平面直角坐标系中,直线![]() 与x轴、y轴分别相交于点A,B,点C在射线OA上,点D在射线OB上,且OD=2OC,以CD的中点为对称中心作△COD的对称图形△DEC.设点C的坐标为(0,n),△DEC在直线AB下方部分的面积为S.
与x轴、y轴分别相交于点A,B,点C在射线OA上,点D在射线OB上,且OD=2OC,以CD的中点为对称中心作△COD的对称图形△DEC.设点C的坐标为(0,n),△DEC在直线AB下方部分的面积为S.
(1)当点E在AB上时,n= ,当点D与点B重合时,n= ;
(2)求S关于n的函数解析式,并直接写出自变量n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年10月l日是中华人民共和国成立70周年的纪念日,天安门广场进行了盛大的阅兵仪式,每一位中华儿女都感到无比骄傲和自豪,“爱我中国,兴我中华”是每一位中华儿女的心声,国庆放假期间,宸宸和点点两位同学想观看电影《我和我的祖国》,由于观影人数较多,他们相约各自在网上购同一场次的票,选座时只剩如图所示的五个空座位了.
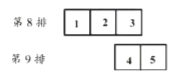
(1)若宸宸随机选择座位,选择座位1的概率为___________;(直接填空)
(2)宸宸和点点各自随机选择座位(同一时间没有其他人在线选票),用列表或画树状图的方法求两位同学选择的座位左右相邻的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是1米,拱桥的跨度为10米,桥洞与水面的最大距离是5米,桥洞两侧壁上各有一盏距离水面4米的景观灯,两盏景观灯之间的水平距离为________米.
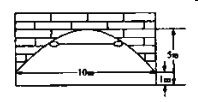
查看答案和解析>>
科目:初中数学 来源: 题型:
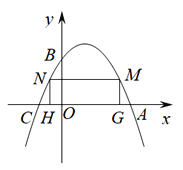
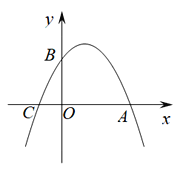
【题目】如图,已知:抛物线![]() 交x轴于A,C两点,交y轴于点B,且OB=2CO.
交x轴于A,C两点,交y轴于点B,且OB=2CO.
(1)求二次函数解析式;
(2)在二次函数图象位于x轴上方部分有两个动点M、N,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;
(3) 抛物线对称轴上是否存在点P,使得△ABP为直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com