
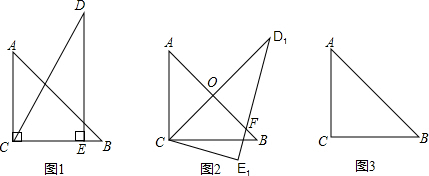
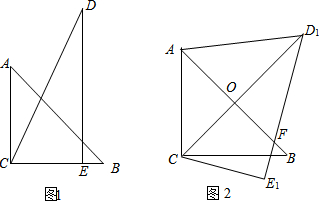
把两个三角形按如图1放置,其中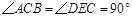 ,
,
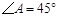 ,
,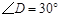 ,且
,且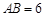 ,
,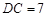 .把△DCE
.把△DCE
绕点C顺时针旋转15°得到△D1CE1,如图2,这时AB与
CD1相交于点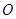 ,与D1E1相交于点F.
,与D1E1相交于点F.
1.求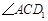 的度数;
的度数;
2.求线段AD1的长;
3.若把△D1CE1绕点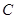 顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.

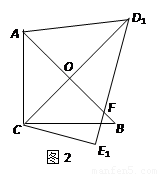
1.如图1,由题意可知:∠BCE1=15°,
∵∠D1CE1=60°,
∴∠D1CB=∠D1CE1—∠D1CB=45°,
又∠ACB=90°,
∴∠ACD1=∠ACB—∠D1CB=45°
2.由(1)知,∠ACD1=45°,
又∠CAB=45°,
∴∠AOD1=∠CAB+∠ACD1=45°∴OC⊥AB,
∵∠BAC=45°,∠ABC=90°—∠BAC=45°,
∴∠ABC=∠BAC,∴AC=BC,
∴OC=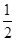 AB=OA=3,∴OD1=CD1—OC=4,
AB=OA=3,∴OD1=CD1—OC=4,
在Rt△AOD1中,∠5=90°,AD1= =5.
=5.
3.点B在△D2CE2内部.
理由如下:设BC(或延长线)交D2E2于点P,则∠PCE2=15°+30°=45°.
在Rt△PCE2中,可求CP=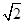
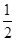 CE2=
CE2= ,
,
在Rt△ABC中,可求BC= ,∵
,∵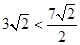 ,即BC
<CP,
,即BC
<CP,
∴点B在△D2CE2内部.
【解析】略


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
(本题满分10分) 把两个三角形按如图1放置,其中∠ACB=∠DEC=90°,
∠CAB=45°,∠CDE=30°,且AB=12,DC=14,把△DCE绕点C顺时针旋转15°
得△D1CE1,如图2,这时AB与CD1相交于点O、与D1E1相交于点F;
1.(1)求∠AC D1的度数;
2.(2)求线段AD1的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
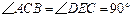 ,
,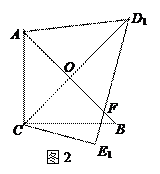
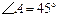 ,
,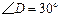 ,且
,且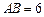 ,
,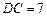 .把△DCE
.把△DCE ,与D1E1相交于点F.
,与D1E1相交于点F. 的度数;
的度数;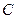 顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.
顺时针再旋转30°得到△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com