
 如图,在△ABC中,BC=12,∠BAC=100°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,求∠EAG的度数和△AEG的周长.
如图,在△ABC中,BC=12,∠BAC=100°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,求∠EAG的度数和△AEG的周长. 分析 在△ABC中,利用三角形内角定理易求∠B+∠C,再根据线段垂直平分线的性质易求∠1=∠B,同理可得∠2=∠C,再结合三角形内角和定理进而可得2(∠B+∠C)+∠EAG=180°,从而可求∠EAG,根据线段垂直平分线的性质得出BE=AE,CG=AG,进而可得出结论.
解答 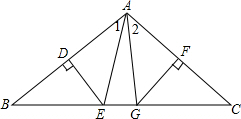 解:∵DE、FG分别是边AB、AC的垂直平分线,BC=12,
解:∵DE、FG分别是边AB、AC的垂直平分线,BC=12,
∴BE=AE,CG=AG,
∴△AEG的周长=AE+AG+EG=BE+CG+EG=BC=12;
在△ABC中,∠BAC=100°,
∴∠B+∠C=180°-100°=80°,
∵DE是AB的垂直平分线,
∴EB=EA,
∴∠1=∠B,
同理可得∠2=∠C,
又∵∠1+∠2+∠B+∠C+∠EAG=180°,
∴2(∠B+∠C)+∠EAG=180°,
∴∠EAG=20°.
点评 本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
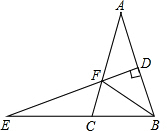 如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=40°,AB+BC=6,则△BCF的周长为6,∠EFC的度数为50°.
如图,△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,∠A=40°,AB+BC=6,则△BCF的周长为6,∠EFC的度数为50°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知b是最小的正整数,且a,b满足(c-5)2+|a+b|=0.请回答题:
已知b是最小的正整数,且a,b满足(c-5)2+|a+b|=0.请回答题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
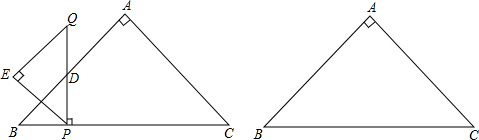
 如图,在旷野上,一个人骑马从A出发,他先使马从A出发,他先使马到草地边l1吃草,再到河边l2饮水,最后返回A,他是怎样走才能使总路程最短?
如图,在旷野上,一个人骑马从A出发,他先使马从A出发,他先使马到草地边l1吃草,再到河边l2饮水,最后返回A,他是怎样走才能使总路程最短?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com