
 如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相交于点M.反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.
如图,在平面直角坐标系中,?OABC的边OA在x轴上,∠COA=30°,OC=8,AC⊥OA,对角线OB与AC相交于点M.反比例函数y=$\frac{k}{x}$(x>0)的图象经过点C.分析 (1)先解Rt△OAC,得出CA=4,OA=4$\sqrt{3}$,那么C(4$\sqrt{3}$,4),再将C点坐标代入反比例函数解析式,即可求解;
(2)先根据平行四边形的对角线互相平分得出AM=$\frac{1}{2}$AC=2.设平移的距离为d,根据平移的性质求出平移后的点M的坐标为(4$\sqrt{3}$+d,2),再根据此时点M在反比例函数的图象上得出(4$\sqrt{3}$+d)×2=16$\sqrt{3}$,解方程即可.
解答 解:(1)在Rt△OAC中,∠COA=30°,OC=8,
∴CA=4,OA=4$\sqrt{3}$,
∴C(4$\sqrt{3}$,4),
∴k=4$\sqrt{3}$×4=16$\sqrt{3}$,
∴反比例函数的表达式为y=$\frac{16\sqrt{3}}{x}$(x>0);
(2)∵点M是?OABC两对角线的交点,
∴AM=$\frac{1}{2}$AC=2.
设平移的距离为d,则平移后的点M的坐标为(4$\sqrt{3}$+d,2),
∴(4$\sqrt{3}$+d)×2=16$\sqrt{3}$,
解得d=4$\sqrt{3}$.
故平移的距离为4$\sqrt{3}$个单位长度.
点评 本题考查了待定系数法求反比例函数解析式,平行四边形的性质,平移的性质,反比例函数图象上点的坐标特征,难度适中.正确求出解析式是解题的关键.


科目:初中数学 来源: 题型:选择题
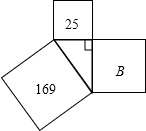 如图,以直角三角形的三边作三个正方形,已知图中两个正方形的面积分别为169,25,则字母B所代表的正方形的面积是( )
如图,以直角三角形的三边作三个正方形,已知图中两个正方形的面积分别为169,25,则字母B所代表的正方形的面积是( )| A. | 144 | B. | 194 | C. | 12 | D. | 169 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 “五一节”期间,杨老师一家自驾游去了离家170千米的某地.如图是他们家的距离y(千米)与汽车行驶时间x(小时)的函数图象,当他们离目的地还有40千米时,汽车一共行驶的时间是2h.
“五一节”期间,杨老师一家自驾游去了离家170千米的某地.如图是他们家的距离y(千米)与汽车行驶时间x(小时)的函数图象,当他们离目的地还有40千米时,汽车一共行驶的时间是2h.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某学校教研组对八年级360名学生就“分组合作学习”方式的支持程度进行了调查,随机抽取了若干名学生进行调查,并制作统计图,据此统计图估计该校八年级学生对“分组合作学习”方式非常喜欢和喜欢的人数约为( )
某学校教研组对八年级360名学生就“分组合作学习”方式的支持程度进行了调查,随机抽取了若干名学生进行调查,并制作统计图,据此统计图估计该校八年级学生对“分组合作学习”方式非常喜欢和喜欢的人数约为( )| A. | 216 | B. | 324 | C. | 288 | D. | 252 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
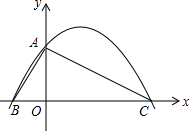 如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
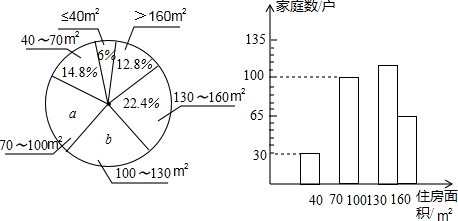
| 住房面和(m2) | ≤40 | 40~70 | 70~100 | 100~130 | 130~160 | >160 |
| $\frac{计划购第二套房的家庭数}{被调查的家庭数}$ | 0 | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{1}{16}$ | $\frac{1}{32}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | k≠0 | B. | k≥-1 | C. | k≥-1且k≠0 | D. | k>-1且k≠0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com