
 某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面$\frac{20}{9}$m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,篮圈距地面3m,设篮球运行的轨迹为抛物线.
某校初三年级的一场篮球比赛中,如图队员甲正在投篮,已知球出手时离地面$\frac{20}{9}$m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,篮圈距地面3m,设篮球运行的轨迹为抛物线.分析 (1)根据抛物线的顶点坐标及球出手时的坐标,可确定抛物线的解析式;
(2)令x=7,求出y的值,与3m比较即可作出判断;
(3)将x=1代入y=-$\frac{1}{9}$(x-4)2+4得y=3进而得出答案.
解答 解:(1)根据题意,球出手点、最高点和篮圈的坐标分别为:
A(0,$\frac{20}{9}$),B(4,4),C(7,3)
设二次函数解析式为y=a(x-h)2+k,
将点(0,$\frac{20}{9}$)代入可得:16a+4=$\frac{20}{9}$,
解得:a=-$\frac{1}{9}$,
∴抛物线解析式为:y=-$\frac{1}{9}$(x-4)2+4;
(2)将C(7,3)点坐标代入抛物线解析式得:
∴-$\frac{1}{9}$(7-4)2+4=3
∴左边=右边
即C点在抛物线上,
∴此球一定能投中.
(3)能拦截成功.
理由:将x=1代入y=-$\frac{1}{9}$(x-4)2+4得y=3
∵3<3.1
∴他能拦截成功.
点评 解答本题的关键是利用待定系数法求出抛物线解析式,注意建立数学模型,培养自己利用数学知识解决实际问题的能力.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm | B. | 10cm | C. | 6cm或4cm | D. | 2cm或10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{x^2}+2x+1}=x+1$ | B. | $\sqrt{{{(-0.1)}^2}}=0.1$ | C. | $-\sqrt{{{(-\frac{1}{3})}^2}}=\frac{1}{3}$ | D. | ${(-\sqrt{3})^2}=-3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 0或2 | C. | 2 | D. | 0或-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 型号 | A | B | C | D | E |
| 进货数量 | 200 | 400 | 500 | 300 | 200 |
| 每个零件赔赚情况 | 赔1.5元 | 赚2元 | 赔0.5元 | 赔1元 | 赚0.2元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
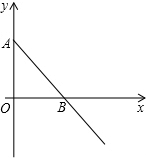 如图,在平面直角坐标系中,直线AB与y轴的正半轴交于点A,与x轴交于点B(2,0),三角形△ABO的面积为2.点Q的坐标是(4,0).动点P从点O出发,以每秒1个单位长度的速度在射线OB上运动,过P作PM⊥x轴交直线AB于M.
如图,在平面直角坐标系中,直线AB与y轴的正半轴交于点A,与x轴交于点B(2,0),三角形△ABO的面积为2.点Q的坐标是(4,0).动点P从点O出发,以每秒1个单位长度的速度在射线OB上运动,过P作PM⊥x轴交直线AB于M.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com