
分析 (1)根据∠C=90°,由勾股定理得AB,利用锐角三角函数,tanA=$\frac{BC}{AC}$,tanB=$\frac{AC}{BC}$,即可得出∠B,∠A;
(2)根据直角三角形的两锐角互余得出∠B=90°-∠A,再根据三角函数的定义即可得出BC=12tanA=12tan22.5°,AB=$\frac{12}{cos22.5°}$.
解答 解:(1)∵∠C=90°,AC=$\sqrt{2}$,BC=$\sqrt{6}$,
∴AC2+BC2=AB2,
∴2+6=AB2,
∴AB=2$\sqrt{2}$,
∴tanA=$\frac{BC}{AC}$=$\frac{\sqrt{6}}{\sqrt{2}}$=$\sqrt{3}$,
∴∠A=60°,
∴∠B=30°,
(2)∵∠A=22.5°,
∴∠B=90°-∠A=90°-22.5°=67.5°,
∵tanA=$\frac{BC}{AC}$=$\frac{a}{b}$,
∵b=12,
∴BC=12tanA=12tan22.5°,
∵cosA=$\frac{AC}{AB}$=$\frac{b}{AB}$,
∴AB=$\frac{12}{cos22.5°}$.
点评 本题考查了解直角三角形,直角三角形的两锐角互余,要熟练掌握好边角之间的关系是解题的关键.


 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:解答题
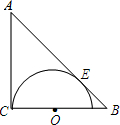 如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$+2,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.求⊙O的半径.
如图,在△ABC中,∠C=90°,AC=BC=2$\sqrt{2}$+2,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.求⊙O的半径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知$\frac{AB}{BE}=\frac{AD}{DE}=\frac{AC}{CE}$,求证:$\frac{AB+BC+CA}{BC}=\frac{AE}{DE}$.
如图,已知$\frac{AB}{BE}=\frac{AD}{DE}=\frac{AC}{CE}$,求证:$\frac{AB+BC+CA}{BC}=\frac{AE}{DE}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
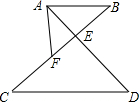 如图所示,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.
如图所示,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
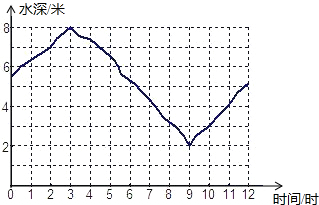 海水受日月的引力而产生潮汐现象,早晨海水上涨叫潮,黄昏海水上涨叫汐,合称潮汐,潮汐与人类的生活有着密切的联系,如图是某港口从0时到12时的水深情况.
海水受日月的引力而产生潮汐现象,早晨海水上涨叫潮,黄昏海水上涨叫汐,合称潮汐,潮汐与人类的生活有着密切的联系,如图是某港口从0时到12时的水深情况.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
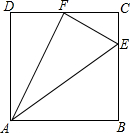 如图,正方形ABCD中,E、F分别是BC、CD上的点,$\frac{CE}{BE}$=$\frac{1}{3}$,CF=FD,连接AE、EF、AF,你能找出图中所有的相似三角形吗?试说明理由.
如图,正方形ABCD中,E、F分别是BC、CD上的点,$\frac{CE}{BE}$=$\frac{1}{3}$,CF=FD,连接AE、EF、AF,你能找出图中所有的相似三角形吗?试说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com