
����Ŀ�� Ϊ������ҵ��ij�������ƶ���С����ҵ���Ż����ߣ�����С����ҵӦ�˶�����ij����ͳ���˸���������1��6�·���ע��С����ҵ������������������Ƴ����µ�����ͳ��ͼ������ͳ��ͼ��
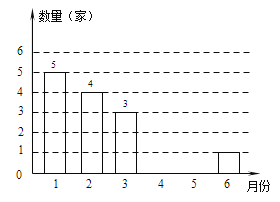

����������Ϣ����������⣺
��1��������1��6����ע��С����ҵһ����__________��;
��2����ȫ����ͳ��ͼ��
��3������ͳ��ͼ�С�4�·ݡ��������ε�Բ�ĽǵĶ���Ϊ ;
��4��������н���1��6�·���ע��С����ҵ����1200�ң�����ȫ�н���1�·���ע��С����ҵ������.
���𰸡���1��20����2������������3��72������4�����н���1�·���ע��С����ҵ������Ϊ300���ң�.
��������
��1������3�·ݵ���ҵ��������ռ�ٷֱȼ��������ע��С����ҵ������
��2�����4��5�·���ע��С����ҵ���������ٲ�ȫͳ��ͼ���ɣ�
��3����360����ԡ�4�·ݡ���ռ�ٷֱȼ��ɣ�
��4���ý���1��6�·���ע��С����ҵ�������ԡ�1�·���ע��С����ҵ����ռ�İٷֱȼ��������.
��1��20
������1��6����ע��С����ҵ��������Ϊ3��15%=20���ң�.
��2��5�·���ע��С����ҵ������Ϊ20��15%=3���ң���
��4�·���ע��С����ҵ��������20��5��4��3��3��1=4���ң���
��ȫ����ͼ��ͼ��ʾ.
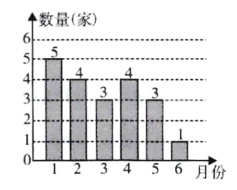
��3��72��
����ͳ��ͼ�С�4�·ݡ��������ε�Բ�ĽǵĶ���Ϊ![]() =72��.
=72��.
��4�����Ƹ��н���1�·���ע��С����ҵ������Ϊ1200��![]() =300���ң�
=300���ң�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����ֱ�������Ӧ�ļ����ڣ�
��2.5��0��8����2��![]() ��
��![]() �� ��0.5252252225����ÿ����5֮����������1��2����
�� ��0.5252252225����ÿ����5֮����������1��2����
��1���������ϣ�{ ��}��
��2���������ϣ�{ ��}��
��3���������ϣ�{ ��}��
��4�����������ϣ�{ ��}��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)15��[3��(��5��4)]��
(2)2.5��(��2)��![]() ��1.5��
��1.5��
(3)2��{8��(��1)��[(��4)��2��(��2)��6��(��6)]}��
(4)(��5)��(��2019)��(��7)��(��2019)��12��2019.
(5)![]() (�ü�㷽��)��
(�ü�㷽��)��
(6)![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�Ķ�������ֱ�ΪA��-2,1����B��-3,-2����C��1��-2��.�ѡ�ABC����ƽ��4����λ���ȣ�������ƽ��3����λ���ȣ��õ���A��B��C�䣮
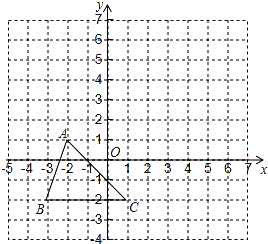
��1����ͼ�л�����A��B��C�䣬��д����A�䣬B�䣬C������ꣻ
��2������A��C��A��A����������AA��C�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪B��C���BC��C��D���CD��D��E���DE.
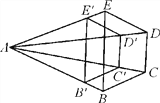
(1)��֤���ı���BCDEλ�����ı���B��C��D��E�䣻
(2)��![]() ��3��S�ı���BCDE��20����S�ı���B��C��D��E��.
��3��S�ı���BCDE��20����S�ı���B��C��D��E��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
����ѧ���ϣ���ʦ��ͬѧ˼���������⣺��ͼ1�����ǰ�һ���ı���ABCD���ı��е�E��F��G��H�������������õ����ı���EFGH��ƽ���ı�����
С����˼������ʱ��������˼·������AC��

���С����˼·������
��1����ֻ�ı�ͼ1���ı���ABCD����״����ͼ2�������ı���EFGH����ƽ���ı�����˵���������ο�С��˼���������������һ��������
��2����ͼ2���ڣ�1���������£�������AC��BD��
�ٵ�AC��BD����ʲô����ʱ���ı���EFGH�����Σ�д�����۲�֤����
�ڵ�AC��BD����ʲô����ʱ���ı���EFGH�Ǿ��Σ�ֱ��д�����ۣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ֱ����ABC�У���BAC��90����AD��BC�ڵ�D��AB��5����E�DZ�AB�ϵĶ��㣨����A��B���غϣ�������DE������D��DF��DE��AC�ڵ�F������EF����H���߶�AD�ϣ���DH��![]() AD������EH��HF����ͼ����Ӱ���ֵ����ΪS1����EHF�������ΪS2����S2��ȡֵ��Χ��_______��
AD������EH��HF����ͼ����Ӱ���ֵ����ΪS1����EHF�������ΪS2����S2��ȡֵ��Χ��_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��DAC��90������ABC�ǵȱ������Σ���PΪ����AD������һ�㣨��P���A���غϣ�������CP�����߶�CP�Ƶ�C˳ʱ����ת60���õ��߶�CQ������QB���ӳ���ֱ��AD�ڵ�E��
��1����ͼ�����QEP�Ķ�����
��2����ͼ������DAC��135������ACP��15������AC��4����BQ�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и���������Ӧ�Ĵ������ڣ�
1��-0.1��-789��25��0��-20��-3.14��![]()
��������{___��}�� ��������{___��}��
��������{____��}�� ��������{____��}��
����������{______��}�� ����������{______��}��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com