
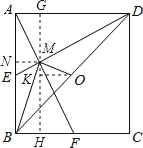
【题目】如图,已知E,F分别为正方形ABCD的边AB,BC的中点,AF与DE交于点M,O为BD的中点,则下列结论:
①∠AME=90°;②∠BAF=∠EDB;③∠BMO=90°;④MD=2AM=4EM;⑤AM=![]() MF.其中正确结论的是( )
MF.其中正确结论的是( )

A. ①③④ B. ②④⑤ C. ①③④⑤ D. ①③⑤
【答案】C
【解析】
根据正方形的性质可得AB=BC=AD,∠ABC=∠BAD=90°,再根据中点定义求出AE=BF,然后利用“边角边”证明△ABF和△DAE全等,根据全等三角形对应角相等可得∠BAF=∠ADE,然后求出∠ADE+∠DAF=∠BAD=90°,从而求出∠AMD=90°,再根据邻补角的定义可得∠AME=90°,得出①正确;
根据中线的定义判断出∠ADE≠∠EDB,然后求出∠BAF≠∠EDB,判断出②错误;
根据直角三角形的性质判断出△AED、△MAD、△MEA三个三角形相似,利用相似三角形对应边成比例可得![]() =2,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=
=2,然后求出MD=2AM=4EM,判断出④正确,设正方形ABCD的边长为2a,利用勾股定理列式求出AF,再根据相似三角形对应边成比例求出AM,然后求出MF,消掉a即可得到AM=![]() MF,判断出③正确.
MF,判断出③正确.
在正方形ABCD中,AB=BC=AD,∠ABC=∠BAD=90°,
∵E、F分别为边AB,BC的中点,
∴AE=BF=![]() BC,
BC,
在△ABF和△DAE中,
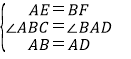 ,
,
∴△ABF≌△DAE(SAS),
∴∠BAF=∠ADE,
∵∠BAF+∠DAF=∠BAD=90°,
∴∠ADE+∠DAF=∠BAD=90°,
∴∠AMD=180°﹣(∠ADE+∠DAF)=180°﹣90°=90°,
∴∠AME=180°﹣∠AMD=180°﹣90°=90°,故①正确;
∵DE是△ABD的中线,
∴∠ADE≠∠EDB,
∴∠BAF≠∠EDB,故②错误;
∵∠BAD=90°,AM⊥DE,
∴△AED∽△MAD∽△MEA,
∴![]() =2,
=2,
∴AM=2EM,MD=2AM,
∴MD=2AM=4EM,故④正确;
设正方形ABCD的边长为2a,则BF=a,
在Rt△ABF中,AF=![]() ,
,
∵∠BAF=∠MAE,∠ABC=∠AME=90°,
∴△AME∽△ABF,
∴![]() ,
,
即![]() ,
,
解得AM=![]() ,
,
∴MF=AF﹣AM=![]() a﹣
a﹣![]() =
=![]() ,
,
∴AM=![]() MF,故⑤正确;
MF,故⑤正确;
如图,过点M作MN⊥AB于N,
则![]() ,
,
即![]() ,
,
解得MN=![]() a,AN=
a,AN=![]() a,
a,
∴NB=AB﹣AN=2a﹣![]() a=
a=![]() a,
a,
根据勾股定理,BM=![]() ,
,
过点M作GH∥AB,过点O作OK⊥GH于K,
则OK=a﹣![]() a=
a=![]() a,MK=
a,MK=![]() a﹣a=
a﹣a=![]() a,
a,
在Rt△MKO中,MO=![]() ,
,
根据正方形的性质,BO=2a×![]() =
=![]() a,
a,
∵BM2+MO2=( ![]() a)2+(
a)2+(![]() a)2=2a2,
a)2=2a2,
BO2=(![]() a)2=2a2,
a)2=2a2,
∴BM2+MO2=BO2,
∴△BMO是直角三角形,∠BMO=90°,故③正确;
综上所述,正确的结论有①③④⑤共4个.
故选:C.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是BC的中点,连接AE并延长交DC的延长线于点F.

(1)求证:AB=CF;
(2)连接DE,若AD=2AB,求证:DE⊥AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P (x,y),若点Q的坐标为(ax+y,x+ay), 其中a为常数,则称点Q是点P的“a级关联点",例如,点P(1,4)的“3级关联点"为Q (3×1+4,1+3×4), 即Q (7,13)。

(1)已知点A (-2,6)的“![]() 级关联点”是点A1,点B的“2级关联点”是B1 (3, 3), 求点A1和点B的坐标:
级关联点”是点A1,点B的“2级关联点”是B1 (3, 3), 求点A1和点B的坐标:
(2)已知点M (m-1, 2m)的“-3级关联点"M位于坐标轴上,求M的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①,在四边形![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() 是
是![]() 的平分线,试判断
的平分线,试判断![]() ,
,![]() ,
,![]() 之间的等量关系.
之间的等量关系.
解决此问题可以用如下方法:延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,易证
,易证![]() 得到
得到![]() ,从而把
,从而把![]() ,
,![]() ,
,![]() 转化在一个三角形中即可判断.
转化在一个三角形中即可判断.
![]() ,
,![]() ,
,![]() 之间的等量关系________;
之间的等量关系________;
(2)问题探究:如图②,在四边形![]() 中,
中,![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,点
,点![]() 是
是![]() 的中点,若
的中点,若![]() 是
是![]() 的平分线,试探究
的平分线,试探究![]() ,
,![]() ,
,![]() 之间的等量关系,并证明你的结论.
之间的等量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P.

(1)若AE=CF;
①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
小明是个爱动脑筋的学生,他在学习了二元一次方程组后遇到了这样一道题目:现有8个大小相同的长方形,可拼成如图1、2所示的图形,在拼图②时,中间留下了一个边长为2的小正方形,求每个小长方形的面积.
小明设小长方形的长为x,宽为y,观察图形得出关于x、y的二元一次方程组,解出x、y的值,再根据长方形的面积公式得出每个小长方形的面积.
解决问题:
(1)请按照小明的思路完成上述问题:求每个小长方形的面积;
(2)某周末上午,小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图3所示.若小明把13个纸杯整齐叠放在一起时,它的高度约是 cm;
(3)小明进行自主拓展学习时遇到了以下这道题目:如图,长方形ABCD中放置8个形状、大小都相同的小长方形(尺寸如图4),求图中阴影部分的面积,请给出解答过程.
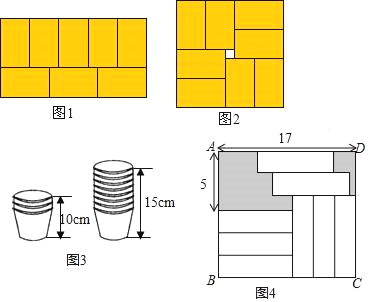
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面坐标系中,ΔABC是等腰直角三角形,∠ABC=90°,AB=BC,点A坐标为(-8,-3),点B坐标为(0,-5),AC交x轴于点D.

(1)求点C和D的坐标;
(2)点M在x轴上,当ΔAMB的周长最小时,求点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com