
 如图,AB是半圆O直径,点C是⊙O上一点,过点O作OD∥AC交BC于点D,在OD的延长线上取一点E,使∠OEB=∠ABC.
如图,AB是半圆O直径,点C是⊙O上一点,过点O作OD∥AC交BC于点D,在OD的延长线上取一点E,使∠OEB=∠ABC.分析 (1)首先由AB是半圆O的直径可以得到∠ACB=90°,由OD∥AC利用平行线的性质可以得到∠EDB=90°,而∠OEB=∠ABC,由此可以证明∠ABC+∠DBE=90°,最后利用切线的判定即可证明题目的结论;
(2)首先解直角三角形求得∠EOB=60°,进而求得∠BOC=120°,然后根据弧长公式即可求解.
解答  (1)证明:∵AB是半圆O的直径,
(1)证明:∵AB是半圆O的直径,
∴∠ACB=90°,
∵OD∥AC,
∴∠EDB=90°,
∴∠OEB+∠DBE=90°,
而∠OEB=∠ABC,
∴∠ABC+∠DBE=90°,
∴∠ABE=90°,
∵OB为半径,
∴BE是⊙O的切线;
(2)解:在RT△OBE中,cos∠EOB=$\frac{OB}{OE}$=$\frac{OA}{OE}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴∠EOB=60°,
连接OC,
∵OD⊥BC,
∴∠COE=∠EOB=60°,
∴∠BOC=120°,
∴弧BC长=$\frac{120π×2}{180}$=$\frac{4}{3}$π.
点评 此题主要考查了圆的切线的性质与判定,垂径定理的应用,解直角三角形和弧长的计算等,属于基础题,关键是掌握各知识点的内容.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:解答题
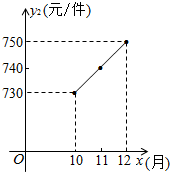 某企业为重庆计算机产业基地提供电脑配件.受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
某企业为重庆计算机产业基地提供电脑配件.受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=1,AC=2,对角线AC、BD相交于点O,直线EF过点O,交 BC于点E,交AD于点F.若四边形AECF恰好为菱形,则∠FOD=30°.
如图,矩形ABCD中,AB=1,AC=2,对角线AC、BD相交于点O,直线EF过点O,交 BC于点E,交AD于点F.若四边形AECF恰好为菱形,则∠FOD=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
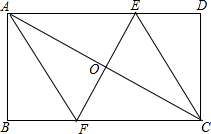 如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.
如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
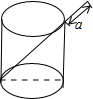 如图,将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形茶杯中,设筷子露在杯子外面的长为acm(茶杯装满水),则a的取值范围是11cm≤a≤12cm.
如图,将一根长24cm的筷子,置于底面直径为5cm,高为12cm的圆柱形茶杯中,设筷子露在杯子外面的长为acm(茶杯装满水),则a的取值范围是11cm≤a≤12cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 现将连续自然数1至2015按图中方式排成一个长方形阵列,用一个长方形框出16个数,如图:
现将连续自然数1至2015按图中方式排成一个长方形阵列,用一个长方形框出16个数,如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com