
分析 (1)通过所获利润等于投资成本×利润率,可直接写出y1、y2与x的关系式.
(2)令y1=y2得关于x的一元一次方程,解方程求出x.
(3)讨论当y1>y2,方案一好;当y1<y2,方案二好.
解答 解:(1)由题意得:y1=20000+(x+20000)×50%
y2=25200-0.2%x.
(2)令y1=y2,得20000+(x+20000)×50%=25200-0.2%x.解方程的x=9760.
所以当该批产品的成本是9760元时,方案一与方案二的获利是一样的.
gai(3)当y1>y2时,即20000+(x+20000)×50%>25200-0.2%x,解得x>9760.
当y1<y2时,即20000+(x+20000)×4.8%<25200-0.2%x,解得x<9760.
当y1=y2时,即20000+(x+20000)×4.8%=25200-0.2%x,解得x=9760.
所以成本大于9760元时,方案一好;当成本小于9760元时,方案二好;成本等于9760元时,方案一、方案二一样.
点评 此题考查了一元一次方程的应用和一元一次不等式的应用,理解所获利润等于投资成本×利润率,根据题意正确列出等量关系和不等关系是本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 cm | B. | 4 cm | C. | 12 cm | D. | 13 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{1}{3}$和 0.333 | B. | -[+(-7)]和-(-7) | C. | -24和 (-2)4 | D. | |3-π|和 π-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
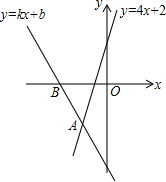 如图,经过点B(-4,0)的直线y=kx+b与直线y=4x+2相交于点A(-2,-2),则不等式4x+2<kx+b<0的解集为-4<x<-2.
如图,经过点B(-4,0)的直线y=kx+b与直线y=4x+2相交于点A(-2,-2),则不等式4x+2<kx+b<0的解集为-4<x<-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com