
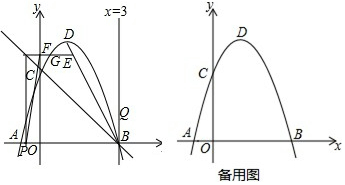
分析 (1)直接把A(-1,0),B(3,0),C(0,3)三点代入抛物线y=ax2+bx+c求得a、b、c得出解析式,进一步求得顶点坐标即可;
(2)连接OH,则四边形HPOF是矩形,利用矩形的性质和垂线段最短求得答案即可;
(3)可用t分别表示出BE、BQ、EQ的长,然后分BE=BQ、BE=EQ、BQ=EQ三种情况,列方程求出t的值.
解答 解:(1)由题意得
$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{c=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$,
∴抛物线y=-x2+2x+3,
顶点D为(1,4);
(2)如图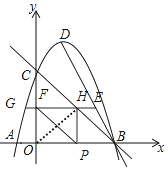 ,
,
连接OH,
∵EF⊥y轴,HP⊥x轴,x轴⊥y轴,
∴四边形HPOF是矩形,
∴PF=OH,
∴当OH最短时,PF最短,
∴OH⊥BC时,PF最短,
可得H的纵坐标为$\frac{3}{2}$,把y=$\frac{3}{2}$代入y=-x2+2x+3,
解得x=$\frac{{2±\sqrt{10}}}{2}$,x=$\frac{{2+\sqrt{10}}}{2}$(舍)
∴G点的坐标($\frac{{2-\sqrt{10}}}{2}$,$\frac{3}{2}$)
(3)存在3个t值能使△BEQ为等腰三角形,
如图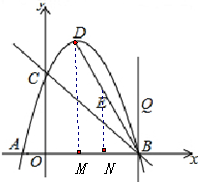 ,
,
DB=2$\sqrt{5}$,yBD=-2x+6,设点E坐标为(t+1,4-2t),Q(3,t)
当BE=BQ时,2$\sqrt{5}$-$\sqrt{5}$t=t,
解得 t=$\frac{{5-\sqrt{5}}}{2}$;
当BE=EQ时(2$\sqrt{5}$-$\sqrt{5}$t)2=(t+1-3)2+(4-2t-t)2,解得$t=\frac{8}{5}$,
当BQ=EQ时t2=(t+1-3)2+(4-2t-t)2,解得$t=\frac{10}{9}$,
所以存在3个t值:t=$\frac{{5-\sqrt{5}}}{2}$.$t=\frac{8}{5}$,$t=\frac{10}{9}$.
点评 此题考查二次函数综合题,待定系数法求函数解析式,矩形的性质,垂线段最短,平面内两点之间的距离等知识的综合运用,注意分类讨论思想的渗透.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com