
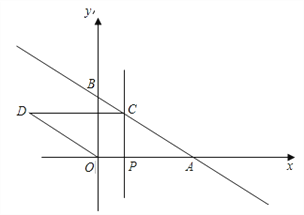
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÖ±Ļßy=kx+bÓėxÖį½»ÓŚA£Ø8£¬0£©£¬ÓėyÖį½»ÓŚB£Ø0£¬6£©£¬µćPŹĒxÖįÕż°ėÖįÉĻµÄŅ»¶Æµć£¬¹żµćP×÷PC”ĶxÖį£¬½»Ö±ĻßABÓŚµćC£¬ŅŌOA£¬ACĪŖ±ß¹¹Ōģ”õOACD£¬ÉčµćPµÄŗį×ų±źĪŖm£®
£Ø1£©ĒóÖ±ĻßABµÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©ČōĖıߊĪOACDĒ”ŹĒĮāŠĪ£¬ĒėĒó³ömµÄÖµ£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬yÖįµÄÉĻŹĒ·ń“ęŌŚµćQ£¬Į¬½įCQ£¬Ź¹µĆ”ĻOQC+”ĻODC=180”ć£®Čō“ęŌŚ£¬Ö±½ÓŠ“³öĖłÓŠ·ūŗĻĢõ¼žµÄµćQµÄ×ų±ź£¬Čō²»“ęŌŚ£¬ŌņĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©y=![]() £»£Ø2£©
£»£Ø2£©![]() »ņ
»ņ![]() £»£Ø3£©Q1(0£¬
£»£Ø3£©Q1(0£¬ ![]() ); Q,2(0£¬-24) ;Q,3(0£¬
); Q,2(0£¬-24) ;Q,3(0£¬ ![]() ).
).
”¾½āĪö”æ£Ø1£©°ŃµćA£Ø8£¬0£©£¬B£Ø0£¬6£©“śČėÖ±Ļßy=kx+b½ā·½³ĢæÉµĆ£»
£Ø2£©øł¾ŻĮāŠĪµÄŠŌÖŹµĆµ½AC=2£¬ÓɵćC£Øm£¬ ![]() m+1£©µĆµ½AP=|2-m|£¬CP=
m+1£©µĆµ½AP=|2-m|£¬CP=![]() +1£¬ĄūÓĆ¹“¹É¶ØĄķĮŠ·½³ĢæÉµĆ£»
+1£¬ĄūÓĆ¹“¹É¶ØĄķĮŠ·½³ĢæÉµĆ£»
£Ø3£©ÓÉĖıߊĪOACDŹĒĮāŠĪ£¬µĆµ½¶Ō½ĒĻąµČ£¬”ĻD=”ĻOAC£¬ÓÉÓŚŹ±QŌŚyÖįÉĻ£¬ĖłÓŠĖıߊĪACQOµÄ¶Ō½Ē»„²¹£¬µĆµ½CQ”ĶAC£¬ĒóµĆÖ±ĻßCQµÄ½āĪöŹ½£¬Ēó³öQµćµÄ×ų±ź.
½ā£ŗ£Ø1£©°ŃµćA£Ø8£¬0£©£¬B£Ø0£¬6£©“śČėÖ±Ļßy=kx+b£¬
æɵĆ![]() £¬½āµĆ
£¬½āµĆ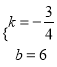 £¬
£¬
”ąÖ±ĻßABµÄŗÆŹż±ķ“ļŹ½ĪŖy=![]() x+6
x+6
(2)¢Łµ±mŌŚOAÉĻ
ÓÉOA=AC
µĆ10- ![]() =8
=8
½āµĆm=![]()
¢Śµ±mŌŚOAŃÓ³¤ĻßÉĻ
ÓÉOA=AC
µĆ![]() -10=8
-10=8
½āµĆm=![]()
Q1(0£¬ ![]() ); Q,2(0£¬-24) ;Q,3(0£¬
); Q,2(0£¬-24) ;Q,3(0£¬ ![]() ).
).
”°µć¾¦”±±¾ĢāĪŖŅ»“ĪŗÆŹżµÄÓ¦ÓĆ£¬Éę¼°“ż¶ØĻµŹż·Ø”¢ĮāŠĪµÄŠŌÖŹ”¢¹“¹É¶ØĄķ¼°·½³ĢĖ¼ĻėµČÖŖŹ¶£¬ŌŚ£Ø1£©ÖŠ×¢Ņā“ż¶ØĻµŹżµÄÓ¦ÓĆ²½Öč£¬ŌŚ£Ø2£©ÖŠĄūÓĆĮāŠĪµÄŠŌÖŹµĆµ½Cµć×ų±źŹĒ½āĢāµÄ¹Ų¼ü£¬ŌŚ£Ø3£©ÖŠĒóµĆQC”ĶABŹĒ½āĢāµÄ¹Ų¼ü.±¾Ģāæ¼²éÖŖŹ¶µć¶ą£¬×ŪŗĻŠŌ½ĻĒ棬ÄѶȏŹÖŠ.


 Ó®ŌŚæĪĢĆĆūŹ¦æĪŹ±¼Ę»®ĻµĮŠ“š°ø
Ó®ŌŚæĪĢĆĆūŹ¦æĪŹ±¼Ę»®ĻµĮŠ“š°ø ĢģĢģĻņÉĻæĪŹ±Ķ¬²½ŃµĮ·ĻµĮŠ“š°ø
ĢģĢģĻņÉĻæĪŹ±Ķ¬²½ŃµĮ·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”ĻDAE=”ĻADE=15”ć£¬DE”ĪAB£¬DF”ĶAB£¬ČōAE=8£¬ŌņDFµČÓŚ£Ø £© 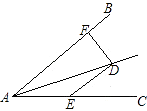
A.5
B.4
C.3
D.2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠø÷Ź½ÄÜÓĆĶźČ«Ę½·½¹«Ź½½ųŠŠ·Ö½āŅņŹ½µÄŹĒ£Ø £©
A.x2+1
B.x2+2x©1
C.x2+x+1
D.x2+4x+4
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĖµ·ØÕżČ·µÄŹĒ£Ø””””£©
A.Ņ»øöÓĪĻ·µÄÖŠ½±øÅĀŹŹĒ![]() £¬ Ōņ×ö5“ĪÕāŃłµÄÓĪĻ·Ņ»¶Ø»įÖŠ½±
£¬ Ōņ×ö5“ĪÕāŃłµÄÓĪĻ·Ņ»¶Ø»įÖŠ½±
B.ĪŖĮĖ½āÉīŪŚÖŠŃ§ÉśµÄŠÄĄķ½”æµĒéæö£¬Ó¦øĆ²ÉÓĆĘÕ²éµÄ·½Ź½
C.ŹĀ¼ž”°Š”Ć÷½ńÄźÖŠæ¼ŹżŃ§æ¼95·Ö”±ŹĒæÉÄÜŹĀ¼ž
D.Čō¼××鏿¾ŻµÄ·½²īS![]() =0.01£¬ŅŅ×鏿¾ŻµÄ·½²īS
=0.01£¬ŅŅ×鏿¾ŻµÄ·½²īS![]() =0.1£¬ŌņŅŅ×鏿¾ŻøüĪȶØ
=0.1£¬ŌņŅŅ×鏿¾ŻøüĪȶØ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”ĻA=15”ć£¬AB=BC=CD=DE=EF£¬Ōņ”ĻDEFµČÓŚ£Ø £© 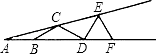
A.90”ć
B.75”ć
C.70”ć
D.60”ć
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼ĖłŹ¾£¬ŌŚ”÷ABCÖŠ£¬AB=AC£¬EŌŚCAŃÓ³¤ĻßÉĻ£¬AE=AF£¬ADŹĒøߣ¬ŹŌÅŠ¶ĻEFÓėBCµÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£® 
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓ¢¹śĀü³¹Ė¹ĢŲ“óѧµÄĮ½Ī»æĘѧ¼ŅŅņĪŖ³É¹¦µŲ“ÓŹÆÄ«ÖŠ·ÖĄė³öŹÆÄ«Ļ©£¬ČŁ»ńĮĖŵ±“¶ūĪļĄķѧ½±.ŹÆÄ«Ļ©µÄĄķĀŪŗń¶Č½ö0.000 000 000 34Ć×£¬½«ÕāøöŹżÓĆæĘѧ¼ĒŹż·Ø±ķŹ¾ĪŖ£Ø £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() ÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬ĒŅOA=2£¬OC=3£®
ÓėxÖį½»ÓŚA”¢BĮ½µć£¬ÓėyÖį½»ÓŚµćC£¬ĒŅOA=2£¬OC=3£®

£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©×÷Rt”÷OBCµÄøßOD£¬ŃÓ³¤ODÓėÅ×ĪļĻßŌŚµŚŅ»ĻóĻŽÄŚ½»ÓŚµćE£¬ĒóµćEµÄ×ų±ź£»
£Ø3£©¢ŁŌŚxÖįÉĻ·½µÄÅ×ĪļĻßÉĻ£¬ŹĒ·ń“ęŌŚŅ»µćP£¬Ź¹ĖıߊĪOBEPŹĒĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬Ēó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
¢ŚŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻ£¬ŹĒ·ń“ęŌŚÉĻµćQ£¬Ź¹µĆ”÷BEQµÄÖܳ¤×īŠ”£æČō“ęŌŚ£¬Ēó³öµćQµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com