
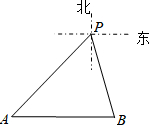
 如图,某天上午,一渔船在我海上指挥中心P的南偏东15°方向的B处遇险,在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援,此时,海口舰与指挥中心P相距10($\sqrt{3}$+1)海里,渔船B在海口舰A的正东方向.求此时渔船B与海口舰A的距离(结果保留根号).
如图,某天上午,一渔船在我海上指挥中心P的南偏东15°方向的B处遇险,在海上指挥中心P的南偏西45°方向A处的海口舰接到求救信号后立刻前往救援,此时,海口舰与指挥中心P相距10($\sqrt{3}$+1)海里,渔船B在海口舰A的正东方向.求此时渔船B与海口舰A的距离(结果保留根号). 分析 过B作BC⊥AP于C,设PC=x,则BC=$\sqrt{3}$x,AC=$\sqrt{3}$x,AB=$\sqrt{6}$x,在Rt△ABC中,根据勾股定理可得PC的长,进一步得到渔船B与海口舰A的距离.
解答 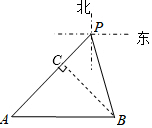 解:过B作BC⊥AP于C,
解:过B作BC⊥AP于C,
由题意知:∠ABC=45°,∠PBC=30°,
设PC=x,
在Rt△PBC中,∠PBC=30°,
则BC=$\sqrt{3}$x,
在Rt△ABC中,∠ABC=45°,
则AC=$\sqrt{3}$x,AB=$\sqrt{6}$x,
∴$\sqrt{3}$x+x=$10({\sqrt{3}+1})$.
解得x=10,
∴AB=10$\sqrt{6}$(海里).
答:B与海口舰A的距离为10$\sqrt{6}$海里.
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将勾股定理的应用的相关知识有机结合,体现了数学应用于实际生活的思想.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:选择题
| A. | m>0 | B. | m≥3 | C. | m≤2 | D. | 2≤m≤3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com