
 如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=10,AB=12.以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.| 1 |
| 2 |
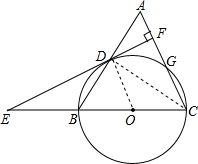 解:如图,连接OD,CD,
解:如图,连接OD,CD,| 1 |
| 2 |
| BC2-BD2 |
| 102-62 |


科目:初中数学 来源: 题型:
 某小区要在一块一边靠墙的空地上修建一个矩形花园,花园的一边靠墙,另三边用长为30m的栅栏围成
某小区要在一块一边靠墙的空地上修建一个矩形花园,花园的一边靠墙,另三边用长为30m的栅栏围成查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 某校对初二年级学生一周做家务的时间进行调查,随机抽查了20名学生,调查结果分为四种类型.A:4小时;B:5小时;C:6小时;D:7小时.将各类人数绘制成如图所示的条形统计图.
某校对初二年级学生一周做家务的时间进行调查,随机抽查了20名学生,调查结果分为四种类型.A:4小时;B:5小时;C:6小时;D:7小时.将各类人数绘制成如图所示的条形统计图.. |
| x |
| x1+x2+…+xn |
| n |
. |
| x |
| 4+5+6+7 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:
近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com