
����Ŀ������ʦ����һ�鳤Ϊ2m����Ϊ1.2m�ľ�����Ƥ����һ���ǵij�������������Ҫ���ĽǸ��õ�һ�������Σ�����Ȳ��ƣ�
��1����������������Ϊ1.28m2����õ��������α߳���
��2����Ҫ�������ij�����ĵ��泤�����ڵ������3���������������з����������ÿƽ���ķ���Ϊ50Ԫ������ÿƽ���ķ���Ϊ200Ԫ���õ��������α߳����ʱ���ܷ�����ͣ����Ϊ���٣�

���𰸡���1���õ��������α߳�Ϊ0.2m����2���õ��������α߳�Ϊ0.4mʱ���ܷ�����ͣ����Ϊ160Ԫ��
��������
��1����õ��������εı߳�Ϊxm�����ݵ�����ε������ʽ�г�һԪ���η��̣���֮�ɵã�
��2���ȸ��ݳ������ڿ���3���ó�x��ȡֵ��Χ���ٸ����ܷ���=������ܷ���+������ܷ����г���������ʽ���䷽�ɶ���ʽ�����ö��κ������������ɵã�
��1����õ��������εı߳�Ϊxm��
�������⣬�ã���2��2x����1.2��2x��=1.28��
��ã�x1=0.2��x2=1.4���ᣩ��
���Բõ��������α߳�Ϊ0.2m��
��2�����������ڿ���3����
��2��2x��3��1.2��2x����
��ã�0��x��0.4��
���ܷ���Ϊw��
�������⣬�ã�w=50��2x��3.2��4x��+200����2��2x����1.2��2x��
=400x2��960x+480
=400��x��1.2��2��96��
���Գ���x=1.2�ҿ������ϣ�
����0��x��0.4ʱ��w��x���������С��
����x=0.4ʱ��wȡ����Сֵ����СֵΪ160Ԫ��
�𣺲õ��������α߳�Ϊ0.4mʱ���ܷ�����ͣ����Ϊ160Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
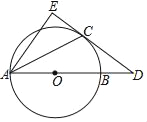
����Ŀ����ͼ����D�ڡ�O��ֱ��AB���ӳ����ϣ�CD�С�O�ڵ�C��AE��CD�ڵ�E
��1����֤��ACƽ�֡�DAE��
��2����AB��6��BD��2����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾������ij��ʱ����Ʒÿ���ɱ�Ϊ20Ԫ�������г����з��֣�������Ʒ��δ��40���ڵ���������m��������ʱ��t���죩�Ĺ�ϵ���㣺m=��2t+96����δ��40���ڣ�ǰ20��ÿ��ļ۸�y1��Ԫ/������ʱ��t���죩�ĺ�����ϵʽΪy1=![]() t+25��1��t��20��tΪ����������20��ÿ��ļ۸�y2��Ԫ/������ʱ��t���죩�ĺ�����ϵʽΪy2=��
t+25��1��t��20��tΪ����������20��ÿ��ļ۸�y2��Ԫ/������ʱ��t���죩�ĺ�����ϵʽΪy2=��![]() t+40��21��t��40��tΪ���������������Ǿ����о�����������Ʒ���й�����
t+40��21��t��40��tΪ���������������Ǿ����о�����������Ʒ���й�����
��1����ֱ�д��δ��40���ڣ�ǰ20��ͺ�20�������������w��Ԫ����ʱ��t�ĺ�����ϵʽ��
��2����Ԥ��δ��40������һ������������������������������Ƕ��٣�
��3����ʵ�����۵�ǰ20���У��ù�˾����ÿ����һ����Ʒ�;���aԪ����a��4����ϣ�����̣���˾ͨ�����ۼ�¼���֣�ǰ20���У�ÿ��۳��������������������ʱ��t���죩�������������a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB��DC��AB��AD���Խ���AC��BD���ڵ�O��ACƽ����BAD������C��CE��AB��AB���ӳ����ڵ�E������OE��
��1����֤���ı���ABCD�����Σ�
��2����AB��![]() ��BD��2����OE�ij���
��BD��2����OE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
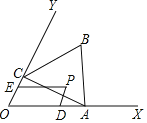
����Ŀ����ͼ����֪��XOY=60������A�ڱ�OX�ϣ�OA=2������A��AC��OY�ڵ�C����ACΪһ���ڡ�XOY�����ȱ�������ABC����P����ABCΧ�ɵ����������ߣ��ڵ�һ�㣬����P��PD��OY��OX�ڵ�D����PE��OX��OY�ڵ�E����OD=a��OE=b����a+2b��ȡֵ��Χ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�ı�OA��x���������ϣ���OC��y���������ϣ�B�������Ϊ(1��3)������O'A'BC'�Ǿ���OABC��B����ʱ����ת�õ��ģ�O'��ǡ����x����������ϣ� O'C'��AB�ڵ�D.
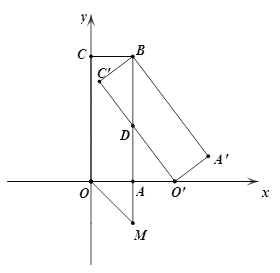
(1)���O'�����꣬���жϡ�O'DB����״��Ҫ˵�����ɣ�
(2)���C'O'����ֱ�ߵĽ���ʽ��
(3)�ӳ�BA��MʹAM=1����(2)����õ�ֱ�����Ƿ���ڵ�P��ʹ�æ�POM�����߶�OMΪֱ�DZߵ�ֱ��������?�����ڣ���ֱ��д��P������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����ACB��ƽ�����ཻ�ڵ�F������F��DE��BC����AB��D����AC��E����ô���н�����ȷ���ǣ��١�BDF����CEF���ǵ��������Σ���DE��BD��CE���ۡ�ADE���ܳ�ΪAB��AC����BD��CE.(����)
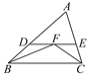
A. �ۢ� B. �٢� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AD��ֱBC�ڵ�D����AD=BC��BC�Ϸ���һ����P����![]() �����P��B��C�������֮����Сʱ����PBC�Ķ���Ϊ�� ��
�����P��B��C�������֮����Сʱ����PBC�Ķ���Ϊ�� ��

A.30��B.45��C.60��D.90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���(a��c)x2��2bx��(a��c)��0������a��b��c�ֱ�Ϊ��ABC���ߵij���
(1)���x����1�Ƿ��̵ĸ������ж���ABC����״����˵�����ɣ�
(2)���������������ȵ�ʵ���������ж���ABC����״����˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com