
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 原式中的1变形为2-1,反复利用平方差公式计算即可得到结果.
解答 解:A=(2+1)(22+1)(24+1)…(22017+1)+1
=(2-1)(2+1)(22+1)(24+1)…(22017+1)+1
=(22-1)(22+1)(24+1)(28+1)…(22017+1)+1
=(24-1)(24+1)(28+1)…(22017+1)+1
=24034,
∵21=2,22=4,23=8,24=16,25=32,…,
∴个位上数字以2,4,8,6为循环节循环,
∵4034÷4=1008…2,
∴A的个位上数字为4,
故选B.
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | a-b=0 | B. | ab=1 | C. | a+b=0 | D. | ab=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
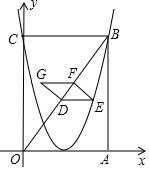 如图,在矩形OABC中,点A在x轴的正半轴,点C在y轴的正半轴.抛物线y=$\frac{16}{9}$x2-$\frac{16}{3}$x+4经过点B,C,连接OB,D是OB上的动点,过D作DE∥OA交抛物线于点E(在对称轴右侧),过E作EF⊥OB于F,以ED,EF为邻边构造?DEFG,则?DEFG周长的最大值为$\frac{243}{40}$.
如图,在矩形OABC中,点A在x轴的正半轴,点C在y轴的正半轴.抛物线y=$\frac{16}{9}$x2-$\frac{16}{3}$x+4经过点B,C,连接OB,D是OB上的动点,过D作DE∥OA交抛物线于点E(在对称轴右侧),过E作EF⊥OB于F,以ED,EF为邻边构造?DEFG,则?DEFG周长的最大值为$\frac{243}{40}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
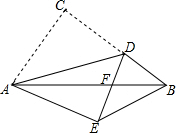 如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为$\frac{3}{2}$或$\frac{3}{4}$.
如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点E处,连接DE交AB于点F,当△DEB是直角三角形时,DF的长为$\frac{3}{2}$或$\frac{3}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com