
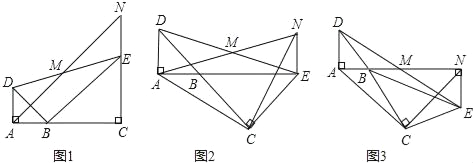
【题目】如图,已知△BAD和△BCE均为等腰直角三角形,∠BAD=∠BCE=90°,点M为DE的中点,过点E与AD平行的直线交射线AM于点N.
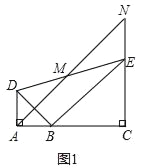
(1)当A,B,C三点在同一直线上时(如图1),直接写出线段AD与NE的数量关系为 .
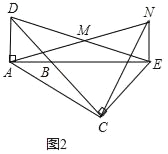
(2)将图1中的△BCE绕点B旋转,当A,B,E三点在同一直线上时(如图2),判断△ACN是什么特殊三角形并说明理由.
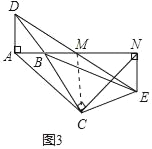
(3)将图1中△BCE绕点B旋转到图3位置,此时A,B,M三点在同一直线上.若AC=3![]() ,AD=1,则四边形ACEN的面积为 .
,AD=1,则四边形ACEN的面积为 .
【答案】(1)AD=AE;(2)△ACN为等腰直角三角形,理由见解析;(3)![]() .
.
【解析】试题分析:(1)证明△ADM和△NEM全等,可得AD=NE.(2)△BAD和△BCE均为等腰直角三角形,证明△ABC和△NEC中,可得∠ABC=∠NEC,△ACN为等腰直角三角形.(3)连接CM,先证明△ADM≌△NEM,△ABC≌△NEC,所以 △ACN为等腰直角三角形,
由(1)可知,△AMD≌△NME,利用S四边形ACNE=S△AMC+S直角梯形MNEC.
试题解析:
解:(1)结论:AD=NE,
理由:如图1,
∵EN∥AD,
∴∠MAD=∠MNE,∠ADM=∠NEM,
∵点M为DE的中点,
∴DM=EM,
在△ADM和△NEM中,
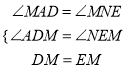 ,
,
∴△ADM≌△NEM,
∴AD=NE.
(2)结论:△ACN为等腰直角三角形.
理由,如图2,
∵△BAD和△BCE均为等腰直角三角形,
∴AB=AD,CB=CE,∠CBE=∠CEB=45°,
∵AD∥NE,
∴∠DAE+∠NEA=180°,
∵∠DAE=90°,
∴∠NEA=90°.
∴∠NEC=135°,
∵A,B,E三点在同一直线上,
∴∠ABC=180°﹣∠CBE=135°,
∴∠ABC=∠NEC,
∵△ADM≌△NEM(已证),
∴AD=NE,
∵AD=AB,
∴AB=NE,
在△ABC和△NEC中,
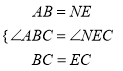 ,
,
∴△ABC≌△NEC,
∴AC=NC,∠ACB=∠NCE,
∴∠ACN=∠BCE=90°,
∴△ACN为等腰直角三角形.
(3)如图3中,连接CM.
∵AD∥NE,M为中点,
∴易得△ADM≌△NEM,
∴AD=NE.
∵AD=AB,
∴AB=NE,
∵AD∥NE,
∴AF⊥NE,
在四边形BCEF中,
∵∠BCE=∠BFE=90°,
∴∠FBC+∠FEC=360°﹣180°=180°
∵∠FBC+∠ABC=180°,
∴∠ABC=∠FEC,
在△ABC和△NEC中,
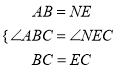 ,
,
∴△ABC≌△NEC,
∴AC=NC,∠ACB=∠NCE,
∴∠ACN=∠BCE=90°,
∴△ACN为等腰直角三角形,
由(1)可知,△AMD≌△NME,
∴AM=MN,AD=NE=1,
∴CM⊥AN,AM=CM=MN,
∵AC=3![]() ,
,
∴AM=CM=MN=3,
∴S四边形ACNE=S△AMC+S直角梯形MNEC=![]() ×3×3+
×3×3+![]() ×(3+1)×3=
×(3+1)×3=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图1,四边形ABCD是平行四边形,E,F是对角线AC上的两点,AE=CF.
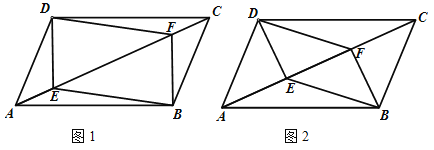
(1)求证:四边形DEBF是平行四边形;
(2)如果AE=EF=FC,请直接写出图中2所有面积等于四边形DEBF的面积的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某玩具厂生产一种玩具,按照控制固定成本降价促销的原则,使生产的玩具能够及时售出,据市场调查:每个玩具按480元销售时,每天可销售160个;若销售单价每降低1元,每天可多售出2个,已知每个玩具的固定成本为360元,问这种玩具的销售单价为多少元时,厂家每天可获利润最多?最多获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
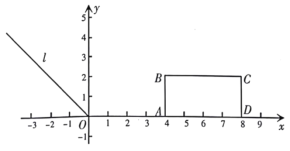
【题目】在平面直角坐标系中,已知长方形![]() ,点
,点![]() ,
,![]() .
.
(1)如图,有一动点![]() 在第二象限的角平分线
在第二象限的角平分线![]() 上,若
上,若![]() ,求
,求![]() 的度数;
的度数;
(2)若把长方形![]() 向上平移,得到长方形
向上平移,得到长方形![]() .
.
①在运动过程中,求![]() 的面积与
的面积与![]() 的面积之间的数量关系;
的面积之间的数量关系;
②若![]() ,求
,求![]() 的面积与
的面积与![]() 的面积之比.
的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“书香长沙2019世界读书日”系列主题活动激发了学生的阅读兴趣,我校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、杜科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
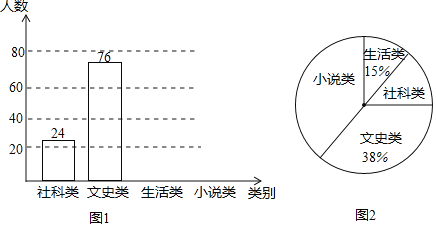
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生3000人,估计该校喜欢“文史类”书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年是中国建国70周年,作为新时期的青少年,我们应该肩负起实现粗国伟大复兴的责任,为了培养学生的爱国主义情怀,我校学生和老师在5月下旬集体乘车去抗日战争纪念馆研学,已知学生的人数是老师人数的12倍多20人,学生和老师总人数有540人.
(1)请求出去抗日战争纪念馆研学的学生和老师的人数各是多少?
(2)如果学校准备租赁A型车和B型车共14辆(其中B型车最多7辆),已知A型车每车最多可以载35人,日租金为2000元,B型车每车最多可以载45人,日租金为3000元,请求出最经济的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市防洪大堤的横截面如图所示,已知AE∥BC,背水坡AB的坡度![]() ,且AB=26米.身高1.8米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度约为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
,且AB=26米.身高1.8米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度约为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)

A. 33米 B. 34米 C. 35米 D. 36米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
与x轴交于B(-3,0)、C(1,0)两点,与y轴交于点A(0,2),抛物线的顶点为D.连接AB,点E是第二象限内的抛物线上的一动点,过点E作EP⊥BC于点P,交线段AB于点F.
(1)求此抛物线的解析式;
(2)过点E作EG⊥AB于点G,Q为线段AC的中点,当△EGF周长最大时,在![]() 轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;
轴上找一点R,使得|RE-RQ|值最大,请求出R点的坐标及|RE-RQ|的最大值;

(3)在(2)的条件下,将△PED绕E点旋转得△ED′P′,当△AP′P是以AP为直角边的直角三角形时,求点P′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com