
【题目】如图,△ABC的内接三角形,P为BC延长线上一点,∠PAC=∠B,AD为⊙O的直径,过C作CG⊥AD于E,交AB于F,交⊙O于G。
(1)判断直线PA与⊙O的位置关系,并说明理由;
(2)求证:AG2=AF·AB;
(3)若⊙O的直径为10,AC=2![]() ,AB=4
,AB=4![]() ,求△AFG的面积.
,求△AFG的面积.

【答案】(1)PA与⊙O相切,理由见解析;(2)证明见解析;(3)3.
【解析】
试题分析:(1)连接CD,由AD为⊙O的直径,可得∠ACD=90°,由圆周角定理,证得∠B=∠D,由已知∠PAC=∠B,可证得DA⊥PA,继而可证得PA与⊙O相切.
(2)连接BG,易证得△AFG∽△AGB,由相似三角形的对应边成比例,证得结论.
(3)连接BD,由AG2=AFAB,可求得AF的长,易证得△AEF∽△ABD,即可求得AE的长,继而可求得EF与EG的长,则可求得答案.
试题解析:解:(1)PA与⊙O相切.理由如下:
如答图1,连接CD,
∵AD为⊙O的直径,∴∠ACD=90°.
∴∠D+∠CAD=90°.
∵∠B=∠D,∠PAC=∠B,∴∠PAC=∠D.
∴∠PAC+∠CAD=90°,即DA⊥PA.
∵点A在圆上,
∴PA与⊙O相切.
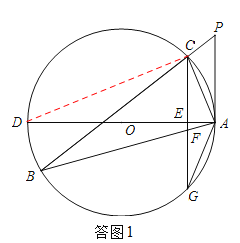
(2)证明:如答图2,连接BG,
∵AD为⊙O的直径,CG⊥AD,∴![]() .∴∠AGF=∠ABG.
.∴∠AGF=∠ABG.
∵∠GAF=∠BAG,∴△AGF∽△ABG.
∴AG:AB=AF:AG. ∴AG2=AFAB.

(3)如答图3,连接BD,
∵AD是直径,∴∠ABD=90°.
∵AG2=AFAB,AG=AC=2![]() ,AB=4
,AB=4![]() ,∴AF=
,∴AF=![]() .
.
∵CG⊥AD,∴∠AEF=∠ABD=90°.
∵∠EAF=∠BAD,∴△AEF∽△ABD. ∴![]() ,即
,即![]() ,解得:AE=2.
,解得:AE=2.
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∴![]() .
.



科目:初中数学 来源: 题型:
【题目】中国首艘完全自主建造的航空母舰于近日正式下水,据悉这艘航母水量将达到50000吨,直追伊丽莎白女王级航母,将500000这个数用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为6cm,点E,M分别是线段BD,AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图①,若点M与点D重合,求证:AF=MN;
(2)如图②,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以![]() cm/s的速度沿BD向点D运动,运动时间为ts.
cm/s的速度沿BD向点D运动,运动时间为ts.
①设BF=ycm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com