
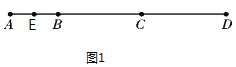
【题目】如图1,![]() 是线段
是线段![]() 上一动点,沿
上一动点,沿![]() 的路线以
的路线以![]() 的速度往返运动1次,
的速度往返运动1次,![]() 是线段
是线段![]() 的中点,
的中点,![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() .
.
![]()
(1)当![]() 时,则线段
时,则线段![]()
![]() ,线段
,线段![]()
![]() .
.
(2)用含![]() 的代数式表示运动过程中
的代数式表示运动过程中![]() 的长.
的长.
(3)在运动过程中,若![]() 的中点为
的中点为![]() ,问
,问![]() 的长是否变化?与点
的长是否变化?与点![]() 的位置是否无关?
的位置是否无关?
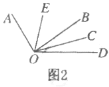
(4)知识迁移:如图2,已知![]() ,过角的内部任一点
,过角的内部任一点![]() 画射线
画射线![]() ,若
,若![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,问∠EOC的度数是否变化?与射线
,问∠EOC的度数是否变化?与射线![]() 的位置是否无关?
的位置是否无关?
【答案】(1)4,3;(2)![]() 或
或![]() ;(3)EC的长不变,与点B的位置无关,EC=5cm;(4)∠EOC的度数不变,与射线OB的位置无关.
;(3)EC的长不变,与点B的位置无关,EC=5cm;(4)∠EOC的度数不变,与射线OB的位置无关.
【解析】
(1)根据线段的和差关系可得;(2)分情况讨论:)①当0≤t≤5时,此时点B从A向D移动;②当5<t≤10时,此时点B从D向A移动;(3)根据线段中点定义可得:EC=EB+BC=![]() AB +
AB +![]() BD =
BD =![]() (AD+BD)=
(AD+BD)=![]() AD;(3)根据角平分线定义可得:∠EOC=∠EOB+∠BOC=
AD;(3)根据角平分线定义可得:∠EOC=∠EOB+∠BOC=![]() (∠AOB+∠BOD)=
(∠AOB+∠BOD)=![]() ∠AOD.
∠AOD.
解:(1)![]() 2×2=4(cm);
2×2=4(cm); ![]() =3(cm)
=3(cm)
![]()
(2)①当0≤t≤5时,此时点B从A向D移动:![]()
②当5<t≤10时,此时点B从D向A移动:![]()
(3)EC的长不变.与点B的位置无关.
∵AB中点为E,C是线段BD的中点,
∴EB=![]() AB,BC=
AB,BC=![]() BD.
BD.
∴EC=EB+BC=![]() AB +
AB +![]() BD =
BD =![]() (AD+BD)=
(AD+BD)=![]() AD
AD
∵AD=10 cm,
∴EC=5cm,与点B的位置无关.
(4)∠EOC的度数不变,与射线OB的位置无关.

∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=![]() ∠AOC,∠COE=
∠AOC,∠COE=![]() ∠BOC,
∠BOC,
∴∠EOC=∠EOB+∠BOC
=![]() (∠AOB+∠BOD)
(∠AOB+∠BOD)
=![]() ∠AOD
∠AOD
∵∠AOD=120°
∴∠EOC=60°,与OB位置无关.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上有![]() 六个点,点
六个点,点![]() 在原点位置,点
在原点位置,点![]() 表示的数为
表示的数为![]() ,已知下表中
,已知下表中![]() 的含义均为前一个点所表示的数与后一个点所表示的数的差,比如
的含义均为前一个点所表示的数与后一个点所表示的数的差,比如![]() 为
为![]() .
.
|
|
|
|
|
|
|
|
|
|
若点![]() 与点
与点![]() 的距离为
的距离为![]() ,则
,则![]() 的值为________
的值为________
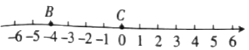
查看答案和解析>>
科目:初中数学 来源: 题型:
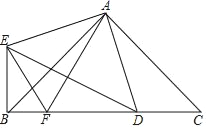
【题目】如图,△ABC和△ADE分别是以BC,DE为底边且顶角相等的等腰三角形,点D在线段BC上,AF平分DE交BC于点F,连接BE,EF.
(1)CD与BE相等?若相等,请证明;若不相等,请说明理由;
(2)若∠BAC=90°,求证:BF2+CD2=FD2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
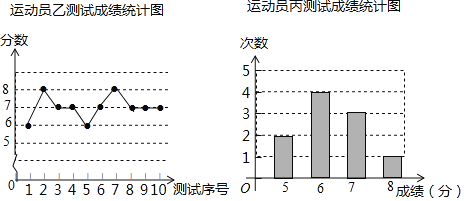
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2018东台西溪半程马拉松”的赛事共有两项:A、“半程马拉松”、 B、“欢乐跑”。小明参加了该项赛事的志愿者服务工作, 组委会随机将志愿者分配到两个项目组.
(1)小明被分配到“半程马拉松”项目组的概率为________.
(2)为估算本次赛事参加“半程马拉松”的人数,小明对部分参赛选手作如下调查:
调查总人数 | 20 | 50 | 100 | 200 | 500 |
参加“半程马拉松”人数 | 15 | 33 | 72 | 139 | 356 |
参加“半程马拉松”频率 | 0.750 | 0.660 | 0.720 | 0.695 | 0.712 |
①请估算本次赛事参加“半程马拉松”人数的概率为_______.(精确到0.1)
②若本次参赛选手大约有3000人,请你估计参加“半程马拉松”的人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:O是直线AB上的一点,![]() 是直角,OE平分
是直角,OE平分![]() .
.
(1)如图1.若![]() .求
.求![]() 的度数;
的度数;
(2)在图1中,![]() ,直接写出
,直接写出![]() 的度数(用含a的代数式表示);
的度数(用含a的代数式表示);
(3)将图1中的![]() 绕顶点O顺时针旋转至图2的位置,探究
绕顶点O顺时针旋转至图2的位置,探究![]() 和
和![]() 的度数之间的关系.写出你的结论,并说明理由.
的度数之间的关系.写出你的结论,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,给出如下定义:对于点P(m,n),若点Q(2﹣m,n﹣1),则称点Q为点P的“δ点”.例如:点(﹣2,5)的“δ点”坐标为(4,4).
(1)某点的“δ点”的坐标是(﹣1,3),则这个点的坐标为 ;
(2)若点A的坐标是(2﹣m,n﹣1),点A的“δ点”为A1点,点A1的“δ点”为A2点,点A2的“δ点”为A3点,…,点A1的坐标是 ;点A2015的坐标是 ;
(3)函数y=﹣x2+2x(x≤1)的图象为G,图象G上所有点的“δ点”构成图象H,图象G与图象H的组合图形记为“图形Ю”,当点(p,q)在“图形Ю”上移动时,若k≤p≤1+2![]() ,﹣8≤q≤1,求k的取值范围
,﹣8≤q≤1,求k的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )
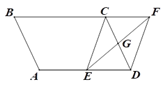
A. 四边形CEDF是平行四边形
B. 当![]() 时,四边形CEDF是矩形
时,四边形CEDF是矩形
C. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
D. 当![]() 时,四边形CEDF是菱形
时,四边形CEDF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面内,将一副直角三角板按如图所示的方式摆放,其中三角形ABC为含60°角的直角三角板,三角形BDE为含45°角的直角三角板.
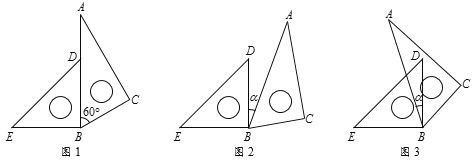
(1)如图1,若点D在AB上,则∠EBC的度数为 ;
(2)如图2,若∠EBC=170°,则∠α的度数为 ;
(3)如图3,若∠EBC=118°,求∠α的度数;
(4)如图3,若0°<∠α<60°,求∠ABE-∠DBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com