
【题目】已知直线CD⊥AB于点O,∠EOF=90°,射线OP平分∠COF.
(1)如图1,∠EOF在直线CD的右侧:
①若∠COE=30°,求∠BOF和∠POE的度数;
②请判断∠POE与∠BOP之间存在怎样的数量关系?并说明理由.
(2)如图2,∠EOF在直线CD的左侧,且点E在点F的下方:
①请直接写出∠POE与∠BOP之间的数量关系;
②请直接写出∠POE与∠DOP之间的数量关系.

【答案】(1)①∠BOF= 30°,∠POE=30°,②∠POE=∠BOP(2)①∠POE=∠BOP②∠POE+∠DOP=270°
【解析】
(1)①根据余角的性质得到∠BOF=∠COE=30°,求得∠COF=90°+30°=120°,根据角平分线的定义即可得到结论;
②根据垂线的性质和角平分线的定义即可得到结论;
(2)①根据角平分线的定义得到∠COP=∠POF,求得∠POE=90°+∠POF,∠BOP=90°+∠COP,于是得到∠POE=∠BOP;
②根据周角的定义即可得到结论.
(1)①∵CD⊥AB,
∴∠COB=90°,
∵∠EOF=90°,
∴∠COE+∠BOE=∠BOE+∠BOF=90°,
∴∠BOF=∠COE=30°,
∴∠COF=90°+30°=120°,
∵OP平分∠COF,
∴∠COP=![]() ∠COF=60°,
∠COF=60°,
∴∠POE=∠COP﹣∠COE=30°;
②CD⊥AB,
∴∠COB=90°,
∵∠EOF=90°,
∴∠COE+∠BOE=∠BOE+∠BOF=90°,
∴∠BOF=∠COE,
∵OP平分∠COF,
∴∠COP=∠POF,
∴∠POE=∠COP﹣∠COE,∠BOP=∠POF﹣∠BOF,
∴∠POE=∠BOP;
(2)①∵∠EOF=∠BOC=90°,
∵PO平分∠COF,
∴∠COP=∠POF,
∴∠POE=90°+∠POF,∠BOP=90°+∠COP,
∴∠POE=∠BOP;
②∵∠POE=∠BOP,∠DOP+∠BOP=270°,
∴∠POE+∠DOP=270°.


科目:初中数学 来源: 题型:
【题目】科技改变生活,手机导航极大方便了人们的出行,如图,小明一家自驾到古镇C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶4千米至B地,再沿北偏东45°方向行驶一段距离到达古镇C,小明发现古镇C恰好在A地的正北方向,求B,C两地的距离. 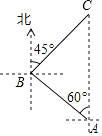
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点A从原点出发向数轴负方向运动,同时动点B也从原点出发向数轴正方向运动,2秒后,两点相距16个单位长度,已知动点A、B的速度比为1:3(速度单位:1个单位长度秒).
![]()
(1)求两个动点运动的速度;
(2)在数轴上标出A、B两点从原点出发运动2秒时的位置;
(3)若表示数0的点记为O,A、B两点分别从(2)中标出的位置同时向数轴负方向运动,再经过多长时间,满足OB=2OA?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBEF是菱形?为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD交于点O,OM⊥AB,
(1)若∠1=∠2,试判断ON与CD的位置关系,并说明理由.
(2)若∠1=![]() ∠BOC,试求∠MOD的度数.
∠BOC,试求∠MOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
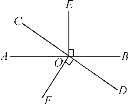
【题目】如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
(1)若OC恰好是∠AOE的平分线,则OA是∠COF的平分线吗?请说明理由;
(2)若∠EOF=5∠BOD,求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国三国时期数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ//AB,则正方形EFGH的边长为.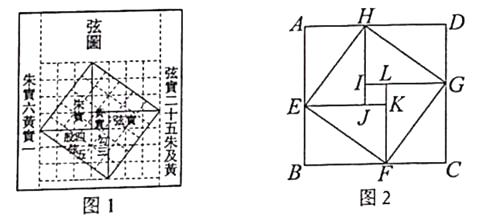
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课题学习中,老师让同学们合作编题.某学习小组受赵爽弦图的启发,编写了下面这道题,请你来解一解.
如图,将矩形ABCD的四边BA、CB、DC、AD分别延长至E、F、G、H,使得AE=CG,BF=DH,连结EF、FG、GH、HE.

(1)求证:四边形EFGH为平行四边形;
(2)若矩形ABCD是边长为1的正方形,且∠FEB=45°,tan∠AEH=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰直角△ABC,点P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径
(1)求证:△APE是等腰直角三角形;
(2)若⊙O的直径为2,求 ![]() 的值
的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com