
【题目】我市要选拔一名教师参加省级评优课比赛:经笔试、面试,结果小潘和小丁并列第一,评委会决定通过摸球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个蓝球,小潘先取出一个球,记住颜色后放回,然后小丁再取出一个球.若两次取出的球都是红球,则小潘胜出;若两次取出的球是一红一蓝,则小丁胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为![]() 的直径,BC为
的直径,BC为![]() 的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是
的切线,弦AD∥OC,直线CD交的BA延长线于点E,连接BD.下列结论:①CD是![]() 的切线;②
的切线;②![]() ;③
;③![]() ;④
;④![]() .其中正确结论的个数有( )
.其中正确结论的个数有( )
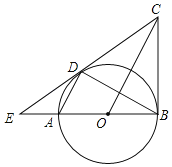
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,点D、E分别在边BC、DC上,AB2 =BE · DC ,DE:EC=3:1 ,F是边AC上的一点,DF与AE交于点G.
(1)找出图中与△ACD相似的三角形,并说明理由;
(2)当DF平分∠ADC时,求DG:DF的值;
(3)如图,当∠BAC=90°,且DF⊥AE时,求DG:DF的值.
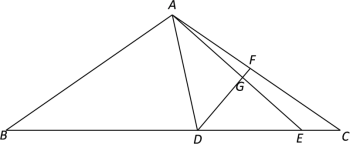
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一条直线把一个平面图形的面积分成相等的两部分,我们把这条直线称为这个平面图形的面积等分线.
问题探究
(1)如图1,△ABC中,点M是AB边的中点,请你过点M作△ABC的一条面积等分线;
(2)如图2,在四边形ABCD中,AD∥BC,CD⊥AD,AD=2,CD=4,BC=6,点P是AB的中点,点Q在CD上,试探究当CQ的长为多少时,直线PQ是四边形ABCD的一条面积等分线;
问题解决
(3)如图3,在平面直角坐标系中,矩形ABCD是某公司将要筹建的花园示意图,A与原点重合,D、B分别在x轴、y轴上,其中AB=3,BC=5,出入口E在边AD上,且AE=1,拟在边BC、AB、CD、上依次再找一个出入口F、G、H,沿EF、GH修两条笔直的道路(路的宽度不计)将花园分成四块,在每一块内各种植一种花草,并要求四种花草的种植面积相等.请你求出此时直线EF和GH的函数表达式.
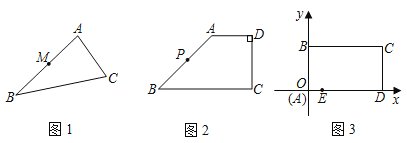
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD边长为3,M、N在对角线AC上且∠MBN=45°,作ME⊥AB于点E、NF⊥BC于点F,反向延长ME、NF交点G,则GEGF的值是( )

A.3B.3![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果直线l把△ABC分割后的两个部分面积相等,且周长也相等,那么就把直线l叫做△ABC的“完美分割线”,已知在△ABC中,AB=AC,△ABC的一条“完美分割线”为直线l,且直线l平行于BC,若AB=2,则BC的长等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边AD,AB的长分别为3,8,E是AB的中点,反比例函数y=![]() 的图象经过点E,与CD交于点F.
的图象经过点E,与CD交于点F.
(1)若点C坐标为(6,0),求m的值及图象经过D,E两点的直线解析式;
(2)若DF﹣DE=2,求反比例函数的表达式.
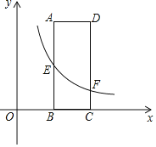
查看答案和解析>>
科目:初中数学 来源: 题型:
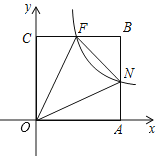
【题目】如图所示,在平面直角坐标系中,正方形OABC的顶点O与原点重合,顶点A,C分别在x轴、y轴上,双曲线y=kx﹣1(k≠0,x>0)与边AB、BC分别交于点N、F,连接ON、OF、NF.若∠NOF=45°,NF=2,则点C的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com