练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知直线y＝－2x＋1与y＝kx交于(－2，a)，则a＝________，k＝________．

    答案：
    解析：

    5,－


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，已知直线y＝－2x＋4与x轴、y轴分别相交于A、C两点，抛物线

    y=-2x+bx+c (a≠0)经过点A、C.

    1.求抛物线的解析式;

    2.设抛物线的顶点为P，在抛物线上存在点Q，使△ABQ的面积等于△APC面积的4倍.求出点Q的坐标;

    3.点M是直线y=-2x+4上的动点，过点M作ME垂直x轴于点E，在y轴（原点除外）上是否存在点F，使△MEF为等腰直角三角形? 若存在,求出点F的坐标及对应的点M的坐标；若不存在，请说明理由

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知直线y＝－2x＋4与x轴、y轴分别相交于A、C两点，抛物线
    y=-2x+bx+c (a≠0)经过点A、C.

    【小题1】求抛物线的解析式;
    【小题2】设抛物线的顶点为P，在抛物线上存在点Q，使△ABQ的面积等于△APC面积的4倍.求出点Q的坐标;
    【小题3】点M是直线y=-2x+4上的动点，过点M作ME垂直x轴于点E，在y轴（原点除外）上是否存在点F，使△MEF为等腰直角三角形? 若存在,求出点F的坐标及对应的点M的坐标；若不存在，请说明理由

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年山东省济宁地区第一学期八年级期末考试数学试卷（带解析） 题型：解答题

    阅读下面的材料：
    在平面几何中，我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数y＝k1x＋b1（k1≠0）的图象为直线l1，一次函数y＝k2x＋b2（k2≠0）的图象为直线l2，若k1＝k2，且b1≠b2，我们就称直线l1与直线l2互相平行.

    解答下面的问题：
    （1）求过点P（1，4）且与已知直线y＝－2x－1平行的直线的函数表达式，并画出直线l的图象；
    （2）设直线l分别与y轴、x轴交于点A、B，如果直线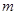：y＝kx＋t ( t＞0)与直线l平行且交x轴于点C，求出△ABC的面积S关于t的函数表达式.

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年福建莆田青璜中学九年级下学期期初考试数学试卷（解析版） 题型：解答题

    如图，已知直线y＝－2x＋4与x轴、y轴分别相交于A、C两点，抛物线y=-2x2+bx+c (a≠0)经过点A、C.

    （1）求抛物线的解析式;

    （2）设抛物线的顶点为P，在抛物线上存在点Q，使△ABQ的面积等于△APC面积的4倍.求出点Q的坐标;

    （3）点M是直线y=-2x+4上的动点，过点M作ME垂直x轴于点E，在y轴（原点除外）上是否存在点F，使△MEF为等腰直角三角形? 若存在,求出点F的坐标及对应的点M的坐标；若不存在，请说明理由.

     

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年山东省济宁地区第一学期八年级期末考试数学试卷（解析版） 题型：解答题

    阅读下面的材料：

    在平面几何中，我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数y＝k1x＋b1（k1≠0）的图象为直线l1，一次函数y＝k2x＋b2（k2≠0）的图象为直线l2，若k1＝k2，且b1≠b2，我们就称直线l1与直线l2互相平行.

    解答下面的问题：

    （1）求过点P（1，4）且与已知直线y＝－2x－1平行的直线的函数表达式，并画出直线l的图象；

    （2）设直线l分别与y轴、x轴交于点A、B，如果直线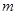：y＝kx＋t ( t＞0)与直线l平行且交x轴于点C，求出△ABC的面积S关于t的函数表达式.

     

    查看答案和解析>>

    同步练习册答案