
分析 (1)利用立方根定义,算术平方根的意义计算即可得到结果.
(2)利用绝对值的意义可得结果;
(3)利用平方根的意义可得结果;
(4)利用立方根的意义可得结果.
解答 解:(1)$\sqrt{(-2)^{2}}$-$\root{3}{8}$+$\root{3}{-\frac{1}{27}}$+$\sqrt{1-\frac{8}{9}}$,
=2-2-$\frac{1}{3}$+$\sqrt{\frac{1}{9}}$,
=-$\frac{1}{3}$+$\frac{1}{3}$,
=0;
(2)|$\sqrt{6}$-$\sqrt{3}$|-|3-$\sqrt{6}$|,
=$\sqrt{6}$-$\sqrt{3}$-(3-$\sqrt{6}$),
=$\sqrt{6}$-$\sqrt{3}$-3+$\sqrt{6}$,
=-$\sqrt{3}$-3;
(3)解方程:(x-3)2=49.
x-3=$±\sqrt{49}$,
x-3=±7,
x=3±7,
x=10或-4;
(4)(x-7)3=27.
x-7=$\root{3}{27}$,
x-7=3,
x=10.
点评 此题考查了实数的运算,主要考查了平方根和立方根的意义,熟练掌握平方根和立方根的意义是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 作平行四边形ABCD的高CE,B是AE的中点,如图.
作平行四边形ABCD的高CE,B是AE的中点,如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发x小时后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.
已知A,B两地公路长300km,甲、乙两车同时从A地出发沿同一公路驶往B地,2小时后,甲车接到电话需返回这条公路上的C处取回货物,于是甲车立即原路返回C,取了货物又立即赶往B地(取货物的时间忽略不计),结果两车同时到达B地.两车的速度始终保持不变,设两车出发x小时后,甲、乙距离A地的距离分别为y1(km)和y2(km),它们的函数图象分别是折线OPQR和线段OR.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
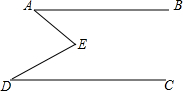 如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC的顶点A、C的坐标分别是(4,7)、(3,2)
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC的顶点A、C的坐标分别是(4,7)、(3,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com