
 ČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬AB=3£¬AD=4£¬µćPŹ±±ßADÉĻŅ»µć£¬½«”÷ABPŃŲÖ±ĻßBPÕŪµž£¬µĆµ½”÷A”äBP£¬Į¬½ÓCA”ä²¢ŃÓ³¤½»ADÓŚµćE£¬ŃÓ³¤PA”ä½»BCµÄŃÓ³¤ĻßÓŚµćF£¬øų³öŅŌĻĀÅŠ¶Ļ£ŗ
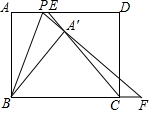
ČēĶ¼£¬¾ŲŠĪABCDÖŠ£¬AB=3£¬AD=4£¬µćPŹ±±ßADÉĻŅ»µć£¬½«”÷ABPŃŲÖ±ĻßBPÕŪµž£¬µĆµ½”÷A”äBP£¬Į¬½ÓCA”ä²¢ŃÓ³¤½»ADÓŚµćE£¬ŃÓ³¤PA”ä½»BCµÄŃÓ³¤ĻßÓŚµćF£¬øų³öŅŌĻĀÅŠ¶Ļ£ŗ·ÖĪö øł¾Ż¾ŲŠĪµÄŠŌÖŹæɵĆAD”ĪBC£¬¾Ż“ĖæɵƔĻAPB=”ĻCBP£¬øł¾ŻÕŪµžµÄŠŌÖŹæɵƔĻAPB=”ĻBPF£¬æɵƵ½”÷BPFŹĒµČŃüČż½ĒŠĪ£»øł¾Ż”ĻA'BP=”ĻA'BC£¬æɵĆA”äBĘ½·Ö”ĻPBC£»øł¾Ż”÷A'BFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬æɵĆBF=$\sqrt{2}$A'B=3$\sqrt{2}$£¬½ų¶ųµĆµ½PF=3$\sqrt{2}$£»øł¾Ż¹“¹É¶ØĄķæÉµĆ£¬Rt”÷PGFÖŠ£¬32+£Ø3+x£©2=£Ø4+x£©2£¬½āµĆx=1£¬ŌŁøł¾ŻBC£ŗFC=4£ŗ1£¬æɵĆ$\frac{{S}_{”÷A”äBC}}{{S}_{”÷A”äCF}}$=4£»µ±µćP”¢A”䔢CŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻŹ±£¬µćPÓėµćEÖŲŗĻ£¬øł¾Ż¹“¹É¶ØĄķæÉµĆ£¬Rt”÷CDEÖŠ£¬32+£Ø4-x£©2=£Øx+$\sqrt{7}$£©2£¬½āµĆx=4-$\sqrt{7}$£¬¼“æÉµĆ³öAE=4-$\sqrt{7}$£®
½ā“š  ½ā£ŗ¢Łµ±AP=$\sqrt{3}$Ź±£¬tan”ĻABP=$\frac{\sqrt{3}}{3}$£¬
½ā£ŗ¢Łµ±AP=$\sqrt{3}$Ź±£¬tan”ĻABP=$\frac{\sqrt{3}}{3}$£¬
”ą”ĻABP=30”ć=”ĻA'BP£¬
”ą”ĻABA'=60”ć£¬”ĻA'BC=30”ć£¬
”ą”ĻA'BP=”ĻA'BC£¬
”ąA”äBĘ½·Ö”ĻPBC£¬¹Ź¢ŁÕżČ·£»
¢Śµ±A”äBĘ½·Ö”ĻABCŹ±£¬”ĻABA'=45”ć=”ĻA'BC£¬
ÓÉÕŪµžæɵƔĻA'BP=$\frac{1}{2}$”ĻABA'=22.5”ć£¬
”ą”ĻPBC=67.5”ć=”ĻAPB=”ĻA'PB£¬
”ąPF=BF£¬
”ąµČŃü”÷BPFÖŠ£¬”ĻF=180”ć-2”Į67.5”ć=45”ć£¬
”ą”÷A'BFŹĒµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ąBF=$\sqrt{2}$A'B=3$\sqrt{2}$£¬
”ąPF=3$\sqrt{2}$£¬¹Ź¢ŚÕżČ·£»
¢ŪČēĶ¼ĖłŹ¾£¬¹żP×÷PG”ĶBCÓŚG£¬
µ±AP=1Ź±£¬BG=1£¬GC=3£¬
ÉčCF=x£¬ŌņBF=4+x£¬GF=3+x£¬
ÓÉ¢ŚæɵĆPF=BF=4+x£¬
¶ųPG=AB=3£¬
”ąRt”÷PGFÖŠ£¬32+£Ø3+x£©2=£Ø4+x£©2£¬
½āµĆx=1£¬
”ąBC£ŗFC=4£ŗ1£¬
”ą$\frac{{S}_{”÷A”äBC}}{{S}_{”÷A”äCF}}$=4£¬¹Ź¢Ū“ķĪó£»
¢ÜČēĶ¼ĖłŹ¾£¬µ±µćP”¢A”䔢CŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻŹ±£¬µćPÓėµćEÖŲŗĻ£¬
ÉčAE=A'E=x£¬ŌņDE=4-x£¬
ÓÉÕŪµžæɵĆAB=A'B=3£¬”ĻBA'C=90”ć£¬¶ųBC=4£¬
”ąRt”÷BCA'ÖŠ£¬A'C=$\sqrt{B{C}^{2}-A'{B}^{2}}$=$\sqrt{7}$£¬
”ąEC=x+$\sqrt{7}$£¬
”ąRt”÷CDEÖŠ£¬32+£Ø4-x£©2=£Øx+$\sqrt{7}$£©2£¬
½āµĆx=4-$\sqrt{7}$£¬
”ąAE=4-$\sqrt{7}$£¬¹Ź¢ÜÕżČ·£®
×ŪÉĻĖłŹö£¬ÕżČ·µÄ½įĀŪŹĒ¢Ł¢Ś¢Ü£¬
¹Ź“š°øĪŖ£ŗ¢Ł¢Ś¢Ü£®
µćĘĄ ±¾ĢāŹōÓŚÕŪµžĪŹĢā£¬Ö÷ŅŖæ¼²éĮĖ¹“¹É¶ØĄķ£¬ÕŪµžµÄŠŌÖŹŅŌ¼°¾ŲŠĪµÄŠŌÖŹµÄ×ŪŗĻÓ¦ÓĆ£¬½āĢāŹ±×¢Ņā£ŗÕŪµžŹĒŅ»ÖÖ¶Ō³Ę±ä»»£¬ĖüŹōÓŚÖį¶Ō³Ę£¬ÕŪµžĒ°ŗóĶ¼ŠĪµÄŠĪדŗĶ“󊔲»±ä£¬Ī»ÖƱä»Æ£¬¶ŌÓ¦±ßŗĶ¶ŌÓ¦½ĒĻąµČ£®


 ĒįĖÉŹī¼Ł×Üø“Ļ°ĻµĮŠ“š°ø
ĒįĖÉŹī¼Ł×Üø“Ļ°ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | 2£¬1 | B£® | 2£¬3 | C£® | 5£¬1 | D£® | 2£¬4 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬CĪŖĻ߶ĪBDÉĻŅ»¶Æµć£¬¹żB”¢D·Ö±š×÷BDµÄ“¹Ļߣ¬Ź¹AB=BC£¬DE=DB£¬Į¬½ÓAD”¢AC”¢BE£¬¹żB×÷ADµÄ“¹Ļߣ¬“¹×ćĪŖF£¬Į¬½ÓCE”¢EF£®
ČēĶ¼£¬CĪŖĻ߶ĪBDÉĻŅ»¶Æµć£¬¹żB”¢D·Ö±š×÷BDµÄ“¹Ļߣ¬Ź¹AB=BC£¬DE=DB£¬Į¬½ÓAD”¢AC”¢BE£¬¹żB×÷ADµÄ“¹Ļߣ¬“¹×ćĪŖF£¬Į¬½ÓCE”¢EF£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 ČēĶ¼£¬Ä³Ń§ÉśŌŚĘģøĖEFÓėŹµŃéĀ„CDÖ®¼äµÄA“¦£¬²āµĆ”ĻEAF=60”ć£¬Č»ŗóĻņ×óŅʶÆ10Ć×µ½B“¦£¬²āµĆ”ĻEBF=30”ć£¬”ĻCBD=45”ć£¬tan”ĻCAD=$\frac{3}{4}$£®
ČēĶ¼£¬Ä³Ń§ÉśŌŚĘģøĖEFÓėŹµŃéĀ„CDÖ®¼äµÄA“¦£¬²āµĆ”ĻEAF=60”ć£¬Č»ŗóĻņ×óŅʶÆ10Ć×µ½B“¦£¬²āµĆ”ĻEBF=30”ć£¬”ĻCBD=45”ć£¬tan”ĻCAD=$\frac{3}{4}$£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® |  | B£® |  | C£® |  | D£® |  |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com