
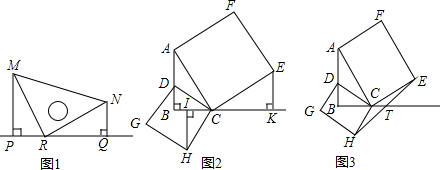
分析 【情景观察】根据等腰直角三角形的性质得到MR=RN,∠MRN=90°,根据余角的性质得到∠PMR=∠NRQ,根据全等三角形的性质得到结论;
【问题探究】根据四边形ACEF是正方形,得到AC=CE,∠ACE=90°根据余角的性质得到∠BAC=∠ECK,根据全等三角形的性质即可得到EK=BC,同理得到BC=HI,等量代换即可得到结论;
【拓展延伸】根据四边形ACEF是矩形,得到∠ACE=90°,根据余角的性质得到∠BAC=∠ECM根据相似三角形的性质得到BC=kEM,同理同理得到BC=kHN,等量代换得到EM=HN,推出△NHT≌△EMT,根据全等三角形的性质即可得到结论.
解答 【情景观察】∵△MRN是等腰直角三角形,
∴MR=RN,∠MRN=90°,
∵MP⊥PQ,NQ⊥PQ,
∴∠MPR=∠NQ=90°,
∴∠PMR+∠MRP=∠MRP+∠NRQ=90°,
∴∠PMR=∠NRQ,
在△MPR与△NRQ中,$\left\{\begin{array}{l}{∠PMR=∠NRQ}\\{∠MPR=∠NRQ}\\{MR=NR}\end{array}\right.$,
∴△MPR≌△NRQ,
∴QN=PR,∠NRQ=∠PMR,
故答案为:PR,∠PMR;
【问题探究】∵四边形ACEF是正方形,
∴AC=CE,∠ACE=90°,
∵EK⊥BK,
∴∠B=∠EKC=90°,
∴∠BAC+∠ACB=∠ACB+∠ECK=90°,
∴∠BAC=∠ECK,
在△ABC与△CEK中,$\left\{\begin{array}{l}{∠BAC=∠KCE}\\{∠B=∠EKC}\\{AC=CE}\end{array}\right.$,
∴△ABC≌△CEK,
∴EK=BC,
∵四边形CDGH是正方形,∴CD=CH,∠DCH=90°,
∵HI⊥BC,
∴∠B=∠CIH=90°,
∴∠DCB+∠ICK=∠ICK+∠CHI=90°,∴∠DCB=∠CHI,
在△DCB与△CHI中,$\left\{\begin{array}{l}{∠B=∠CIH}\\{∠BCD=∠CHI}\\{CD=CH}\end{array}\right.$,∴△DCB≌△CHI,
∴BC=HI,
∴EK=IH;
【拓展延伸】如图3,过E作EM⊥BC于M,过H作HN⊥BC于N,
∵四边形ACEF是矩形,
∴∠ACE=90°,
∴∠BAC+∠ACB=∠ACB+∠ECM=90°,
∴∠BAC=∠ECM,∴△ACB∽△ECM,
∴$\frac{BC}{EM}=\frac{AC}{CE}$=k,
∴BC=kEM,
同理△BCD∽△NHC,
∴$\frac{BC}{HN}=\frac{CD}{CH}$=K,
∴BC=kHN,
∴EM=HN,
在△NHT与△EMT中,$\left\{\begin{array}{l}{∠HNT=∠EMT=90°}\\{∠NTH=∠MTE}\\{HN=EM}\end{array}\right.$,
∴△NHT≌△EMT,
∴ET=HT.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,正方形的性质,矩形的性质,余角的性质,(3)证得△ACB∽△ECM,△BCD∽△NHC是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,AB=AE,BE的延长线分别交AD、AC的延长线于点F、G.
如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,AB=AE,BE的延长线分别交AD、AC的延长线于点F、G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某移动公司近日推出了如下两种月收费方式.
某移动公司近日推出了如下两种月收费方式.| 收费方式 | 月租费/元 | 赠送通话时间/分钟 | 超时费/(元/分钟) |
| A | k | l | 0.2 |
| B | m | n | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 6ab-b=6a | B. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ | C. | a8÷a2=a4 | D. | (a2b)3=a6b3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<$\frac{1}{3}$ | B. | m<-$\frac{1}{3}$ | C. | m>$\frac{1}{3}$ | D. | m>-$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
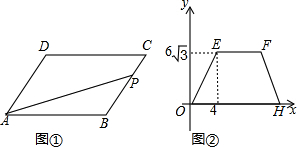
| A. | 11 | B. | 14 | C. | 8+$\frac{3}{2}\sqrt{3}$ | D. | 8+3$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
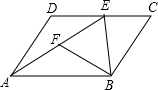 如图,在?ABCD中,过点B作BE⊥DC于点E,连接AE,F为AE上一点,且∠BFE=∠C.
如图,在?ABCD中,过点B作BE⊥DC于点E,连接AE,F为AE上一点,且∠BFE=∠C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com