
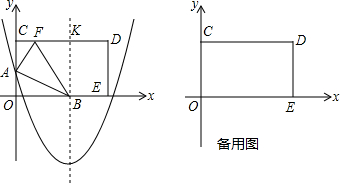
分析 (1)①根据四边形OCKB是矩形以及对称轴公式即可解决问题.
②在RT△BKF中利用勾股定理即可解决问题.
③设OA=AF=x,在RT△ACF中,AC=8-x,AF=x,CF=4,利用勾股定理即可解决问题.
(2)不变.S1•S2=289.由△GHN∽△MHG,得$\frac{GH}{MH}$=$\frac{HN}{GH}$,得到GH2=HN•HM,求出GH2,根据S1•S2=$\frac{1}{2}$•OG•HN•$\frac{1}{2}$•OG•HM即可解决问题.
解答 解:(1)如图1中,①∵抛物线y=$\frac{3}{20}$x2-3x+m的对称轴x=-$\frac{b}{2a}$=10,
∴点B坐标(10,0),
∵四边形OBKC是矩形,
∴CK=OB=10,KB=OC=8,
故答案分别为10,0,8,10.
②在RT△FBK中,∵∠FKB=90°,BF=OB=10,BK=OC=8,
∴FK=$\sqrt{B{F}^{2}-B{K}^{2}}$=6,
∴CF=CK-FK=4,
∴点F坐标(4,8).
③设OA=AF=x,
在RT△ACF中,∵AC2+CF2=AF2,
∴(8-x)2+42=x2,
∴x=5,
∴点A坐标(0,5),代入抛物线y=$\frac{3}{20}$x2-3x+m得m=5,
∴抛物线为y=$\frac{3}{20}$x2-3x+5.
(2)不变.S1•S2=289.
理由:如图2中,在RT△EDG中,∵GE=EO=17,ED=8,
∴DG=$\sqrt{G{E}^{2}-D{E}^{2}}$=$\sqrt{1{7}^{2}-{8}^{2}}$=15,
∴CG=CD-DG=2,
∴OG=$\sqrt{O{C}^{2}+C{G}^{2}}$=$\sqrt{{8}^{2}+{2}^{2}}$=2$\sqrt{17}$,
∵GP⊥OM,MH⊥OG,
∴∠NPM=∠NHG=90°,
∵∠HNG+∠HGN=90°,∠PNM+∠PMN=90°,∠HNG=∠PNM,
∴∠HGN=∠NMP,
∵∠NMP=∠HMG,∠GHN=∠GHM,
∴△GHN∽△MHG,
∴$\frac{GH}{MH}$=$\frac{HN}{GH}$,
∴GH2=HN•HM,
∵GH=OH=$\sqrt{17}$,
∴HN•HM=17,
∵S1•S2=$\frac{1}{2}$•OG•HN•$\frac{1}{2}$•OG•HM=($\frac{1}{2}$•2$\sqrt{17}$)2•17=289.
点评 本题考查二次函数综合题、矩形的性质、翻折变换相似三角形的判定和性质、勾股定理等知识,解题的关键是证明△GHN∽△MHG求出HN•HM的值,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
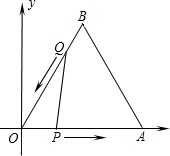 如图,等边△ABO放置在平面直角坐标系中,OA=4,动点P、Q同时从O、B两点出发,分别沿OA、BO方向匀速运动,它们的速度均为每秒1个单位长度,当点P到达点A时,P、Q两点停止运动,设点P的运动时间为x(s)(0<x<4),解答下列问题:
如图,等边△ABO放置在平面直角坐标系中,OA=4,动点P、Q同时从O、B两点出发,分别沿OA、BO方向匀速运动,它们的速度均为每秒1个单位长度,当点P到达点A时,P、Q两点停止运动,设点P的运动时间为x(s)(0<x<4),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | P(C)<P(A)<P(B) | B. | P(B)<P(C)<P(A) | C. | P(C)<P(B)<P(A) | D. | P(B)<P(A)<P(C) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com