
【题目】某教育网站对下载资源规定如下:若注册VIP用户,则下载每份资源收![]() 元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收
元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收![]() 元,不收其它费用
元,不收其它费用
![]() 分别写出注册VIP用户的收费
分别写出注册VIP用户的收费![]() 元
元![]() 和注册普通用户
和注册普通用户![]() 元
元![]() 与下载数量
与下载数量![]() 份
份![]() 之间的函数关系式
之间的函数关系式
![]() 某学校每年要下载1500份资源,那么注册哪种用户比较合算?
某学校每年要下载1500份资源,那么注册哪种用户比较合算?
![]() 一年内下载多少份资源是两种用户收费一样?
一年内下载多少份资源是两种用户收费一样?
【答案】(1)![]() 用户:
用户:![]() ,普通用户:
,普通用户:![]() .(2)当
.(2)当![]() 时,注册普通用户比较合算;(3)当下载量为2500份时,注册两种用户的收费相等.
时,注册普通用户比较合算;(3)当下载量为2500份时,注册两种用户的收费相等.
【解析】
(1)依据若注册VIP用户,则下载每份资源收0.2元,另外每年收500元的VIP会员费,若注册普通用户,则下载每份资源收0.4元,不收其它费用,即可得到VIP用户的收费(y1元)和注册普通用户y2(元)与下载数量x(份)之间的函数关系式;
(2)依据x=1500,分别求得y1和 y2的值,即可得到结论;
(3)由y1=y2得:0.2x+500=0.4x,进而得出当下载量为2500份时,注册两种用户的收费相等.
解:![]() 用户:
用户:![]() ,
,
普通用户:![]() .
.
![]() 当
当![]() 时,
时,![]() 元
元![]()
![]() 元
元![]()
![]()
![]() 当
当![]() 时,注册普通用户比较合算;
时,注册普通用户比较合算;
![]() 由
由![]()
![]() 得:
得:![]() ,
,
解得:![]() ,
,
所以当下载量为2500份时,注册两种用户的收费相等.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】【阅读新知】
三角形中任何一边的平方等于其它两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
即:如图1,.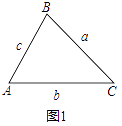
在△ABC中,已知AB=c,BC=a,CA=b,则有:
a2=b2+c2﹣2bccosA,b2=a2+c2﹣2accosB,c2=a2+b2﹣2abcosC
利用这个正确结论可求解下列问题:
例在△ABC中,已知a=2 ![]() ,b=2
,b=2 ![]() ,c=
,c= ![]() ,求∠A.
,求∠A.
解:∵a2=b2+c2﹣2bccosA,
cosA= ![]() =
= ![]() =
= ![]() .
.
∴∠A=60°.
【应用新知】
(1)选择题:在△ABC中,已知b=ccosA,a=csinB,那么△ABC是( ).
A.等边三角形
B.等腰三角形
C.等腰直角三角形
D.直角三角形
(2)如图2,
某客轮在A处看港口D在客轮的北偏东50°,A处看灯塔B在客轮的北偏西30°,距离为2 ![]() 海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点G为BC边的中点,点H在AF上,动点P以每秒1cm的速度沿图1的边运动,运动路径为![]() ,相应的
,相应的![]() 的面积
的面积![]() 关于运动时间
关于运动时间![]() 的函数图象如图2,若
的函数图象如图2,若![]() ,则下列结论正确的个数有
,则下列结论正确的个数有![]()
![]()
![]() 图1中BC长4cm;
图1中BC长4cm;![]() 图1中DE的长是3cm;
图1中DE的长是3cm;![]() 图2中点M表示4秒时的y值为
图2中点M表示4秒时的y值为![]() ;
;![]() 图2中的点N表示12秒时y值为
图2中的点N表示12秒时y值为![]() .
.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“宜居襄阳”是我们的共同愿景,空气质量备受人们关注.我市某空气质量监测站点检测了该区域每天的空气质量情况,统计了2013年1月份至4月份若干天的空气质量情况,并绘制了如下两幅不完整的统计图. 
请根据图中信息,解答下列问题:
(1)统计图共统计了天的空气质量情况;
(2)请将条形统计图补充完整;;空气质量为“优”所在扇形的圆心角度数是;
(3)从小源所在环保兴趣小组4名同学(2名男同学,2名女同学)中,随机选取两名同学去该空气质量监测站点参观,则恰好选到一名男同学和一名女同学的概率是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图,在
如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,可求得
,可求得![]() ______.
______.
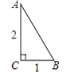
![]() 如图,直径为1个单位长度的圆从原点O沿数轴向右滚动一周,圆上的一点
如图,直径为1个单位长度的圆从原点O沿数轴向右滚动一周,圆上的一点![]() 滚动时与点O重合
滚动时与点O重合![]() 由原点到达点
由原点到达点![]() ,则
,则![]() 的长度是______.
的长度是______.

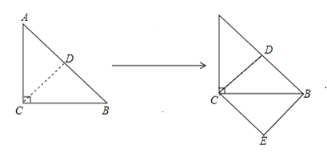
![]() 如图,
如图,![]() 是一个等腰直角三角形,它的面积是2,把它沿着斜边的高线剪开拼成如图正方形EBDC,则这个正方形的边长是______.
是一个等腰直角三角形,它的面积是2,把它沿着斜边的高线剪开拼成如图正方形EBDC,则这个正方形的边长是______.
![]() 请你在
请你在![]() 的网格图中
的网格图中![]() 每个小正方形边长均为
每个小正方形边长均为![]() ,画出一条长为
,画出一条长为![]() 的线段;
的线段;

![]() 学习了实数后,我们知道数轴上的点与实数是一一对应的关系
学习了实数后,我们知道数轴上的点与实数是一一对应的关系![]() 那么请你在图的数轴上画出表示
那么请你在图的数轴上画出表示![]() 的点
的点![]() 保留作图痕迹
保留作图痕迹![]() .
.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B,C重合),现将△PCD沿直线PD折叠,使点C落下点C1处;作∠BPC1的平分线交AB于点E.设BP=x,BE=y,那么y关于x的函数图象大致应为( )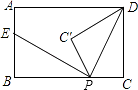
A.
B. 
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程:
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;
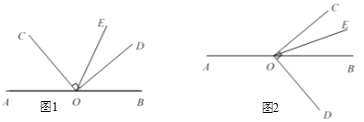
解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =![]() ∠BOC ( ).
∠BOC ( ).
∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知双曲线y= ![]() (k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(k>0)与直线y=k′x交于A、B两点,点A在第一象限,试回答下列问题:
(1)若点A的坐标为(3,1),则点B的坐标为;当x满足:时, ![]() ≤k′x;
≤k′x;
(2)如图2,过原点O作另一条直线l,交双曲线y= ![]() (k>0)于P,Q两点,点P在第一象限.
(k>0)于P,Q两点,点P在第一象限.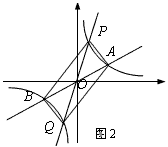
四边形APBQ一定是;
(3)若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积.
(4)设点A,P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出m,n应满足的条件;若不可能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com