
【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车 | 乙种客车 | |
载客量(座/辆) | 60 | 45 |
租金(元/辆) | 550 | 450 |
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
【答案】(1)函数表达式是y=100x+3150;(2)当甲种客车有5辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是3650元.
【解析】试题分析:(1)y=租甲种车的费用+租乙种车的费用,由题意代入相关数据即可得;
(2)根据题意确定出x的取值范围,再根据一次函数的增减性即可得.
试题解析:(1)由题意,得
y=550x+450(7﹣x),化简,得y=100x+3150,即y(元)与x(辆)之间的函数表达式是y=100x+3150;
(2)由题意,得60x+45(7﹣x)≥380,解得,x≥![]() .
.
∵y=100x+3150,∴k=100>0,∴x=5时,租车费用最少,最少为:y=100×5+3150=3650(元),
即当甲种客车有5辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是3650元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
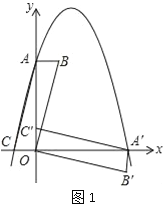
【题目】在平面直角坐标系中,平行四边形ABOC如图放置,点A、C的坐标分别是(0,4)、(﹣1,0),将此平行四边形绕点O顺时针旋转90°,得到平行四边形A′B′OC′.
(1)若抛物线经过点C、A、A′,求此抛物线的解析式;
(2)点M时第一象限内抛物线上的一动点,问:当点M在何处时,△AMA′的面积最大?最大面积是多少?并求出此时M的坐标;
(3)若P为抛物线上一动点,N为x轴上的一动点,点Q坐标为(1,0),当P、N、B、Q构成平行四边形时,求点P的坐标,当这个平行四边形为矩形时,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通网络的不断完善.旅游业持续升温,据统计,在今年“五一”期间,某风景区接待游客403000人,这个数据用科学记数法表示为( )
A.403×103
B.40.3×104
C.4.03×105
D.0.403×106
查看答案和解析>>
科目:初中数学 来源: 题型:
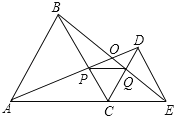
【题目】如图,C为线段AE上一动点(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.
恒成立的结论有 .(把你认为正确的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com