
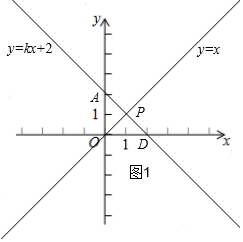
 已知直线l:y=kx+2与直线m:y=x相交于P点,且点P的横坐标为1,直线l与x轴交于点D,与反比例函数G:y=$\frac{n}{x}$的图象交于点M,N(点M在点N的左侧),若DM+DN<3$\sqrt{2}$,求n的取值范围.
已知直线l:y=kx+2与直线m:y=x相交于P点,且点P的横坐标为1,直线l与x轴交于点D,与反比例函数G:y=$\frac{n}{x}$的图象交于点M,N(点M在点N的左侧),若DM+DN<3$\sqrt{2}$,求n的取值范围. 分析 先求P点的坐标(1,1),代入y=kx+2中可求得k=-1,分两种情况进行讨论:①当n>0时,如图2,求出AD=2$\sqrt{2}$,所以交点M、N都能满足DM+DN<3$\sqrt{2}$,所以列方程求△>0即可;②当n<0时,如图3,因为n越小离两坐标轴越远,所以求
DM+DN=3$\sqrt{2}$时的n值即可.
解答 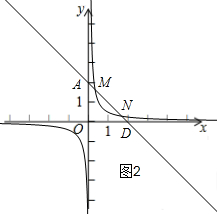
 解:如图1,当x=1时,y=1,
解:如图1,当x=1时,y=1,
∴P(1,1),
把P(1,1)代入y=kx+2中得:1=k+2,
k=-1,
∴直线l:y=-x+2,
分两种情况:
①当n>0时,如图2,
∵直线l:y=-x+2与x轴交于D(2,0),与y轴交于A(0,2),
∴AD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
∵DM+DN<3$\sqrt{2}$,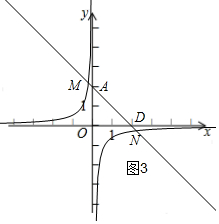
∴只要y=-x+2与y=$\frac{n}{x}$有两个交点即可,
∴-x+2=$\frac{n}{x}$,
x2-2x+n=0,
b2-4ac=4-4n>0,
n<1,
∴0<n<1;
②当n<0时,如图3,
当DM+DN=3$\sqrt{2}$时,AM+DN=$\frac{\sqrt{2}}{2}$,
∵直线l:y=-x+2与x轴交于D(2,0),与y轴交于A(0,2),
则M(-$\frac{1}{2}$,$\frac{5}{2}$),
xy=n=-$\frac{1}{2}$×$\frac{5}{2}$=-$\frac{5}{4}$,
∴-$\frac{5}{4}$<n<0,
综上所述:n的取值范围是0<n<1或-$\frac{5}{4}$<n<0.
点评 本题考查了一次函数、反比例函数的交点问题,有难度,本题采用了分类讨论的思想,反比例函数系数的不同与一次函数交点的距离也不同,根据数形结合的思想进行计算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以每秒3cm的速度向点B移动,点Q以每秒12cm测得速度向点D移动,当点P到达点B处时,两点均停止移动
如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以每秒3cm的速度向点B移动,点Q以每秒12cm测得速度向点D移动,当点P到达点B处时,两点均停止移动查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com