
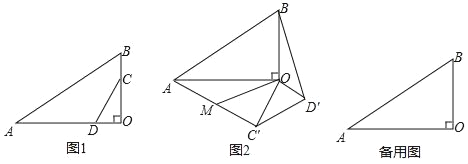
【题目】如图1,在Rt△AOB中,∠AOB=90°,∠OAB=30°,点C在线段OB上,OC=2BC,AO边上的一点D满足∠OCD=30°.将△OCD绕点O逆时针旋转α度(90°<α<180°)得到△OC′D′,C,D两点的对应点分别为点C′,D′,连接AC′,BD′,取AC′的中点M,连接OM.
(1)如图2,当C′D′∥AB时,α= °,此时OM和BD′之间的位置关系为 ;
(2)画图探究线段OM和BD′之间的位置关系和数量关系,并加以证明.
【答案】(1)150,垂直;(2)OM⊥BD′,OM=![]() BD′
BD′
【解析】
(1)根据平行线的性质得到∠ABD′+∠C′D′B=180°,
根据周角的定义即可得到结论;
(2)取AO的中点E,连接ME,延长MO交BD′于N,根据三角形的中位线的性质得到EM∥OC′,EM=![]() OC′,根据相似三角形的性质得到∠AOM=∠2,
OC′,根据相似三角形的性质得到∠AOM=∠2,![]() ,根据垂直的定义即可得到结论.
,根据垂直的定义即可得到结论.
解:(1)∵C′D′∥AB,
∴∠ABD′+∠C′D′B=180°,
∵∠ABO=∠C′D′O=60°,
∴∠OBD′+∠BD′O=60°,
∴∠BOD′=120°,
∴∠BOC′=360°﹣90°﹣90°﹣120°=150°,
∴α=150°,此时,OM⊥BD′;
故答案为:150,垂直;
(2)OM⊥BD′,OM=![]() BD′,
BD′,
证明:取AO的中点E,连接ME,延长MO交BD′于N,
∵AC′的中点M,
∴EM∥OC′,EM=![]() OC′,
OC′,
∴∠OEM+∠AOC′=180°,∵∠AOB=∠C′OD′=90°,
∴∠BOD′+′AOC′=180°,
∴∠OEM=∠BOD′,
∵∠OAB=∠OC′D′=30°,
∴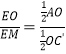 =
=![]() =
=![]() =
=![]() ,
,
∴![]() ,
,
∴△EOM∽△OBD′,
∴∠AOM=∠2,![]() ,
,
即OM=![]() BD′,
BD′,
∵∠AOB=90°,
∴∠AOM+∠3=180°﹣∠AOB=90°,∴∠2+∠3=90°,
∴OM⊥BD′.


科目:初中数学 来源: 题型:
【题目】今年猪肉价格受非洲猪瘟疫情影响,有较大幅度的上升,为了解某地区养殖户受非洲猪瘟疫情感染受灾情况,现从该地区建档的养殖户中随机抽取了部分养殖户进行了调查(把调查结果分为四个等级:A级:非常严重;B级:严重;C级:一般;D级:没有感染),并将调查结果绘制成如下两幅不完整的统计图.请根据统计图中的信息解决下列问题:
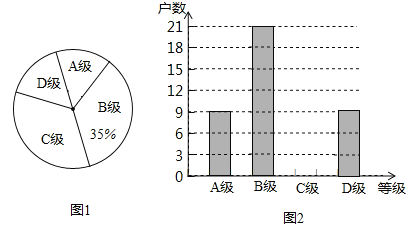
(1)本次抽样调查的养殖户的总户数是 ;把图2条形统计图补充完整.
(2)若该地区建档的养殖户有1500户,求非常严重与严重的养殖户一共有多少户?
(3)某调研单位想从5户建档养殖户(分别记为a,b,c,d,e)中随机选取两户,进一步跟踪监测病毒传播情况,请用列表或画树状图的方法求出选中养殖户e的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装专卖店,为了吸引顾客,在“六一”儿童节当天举办了甲、乙两种品牌童装有奖酬宾活动,凡购物满100元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同.摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如表).
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满100元,若只考虑获得最多的礼品券,请你帮助分析选择购买哪种品牌的童装?并说明理由.
甲种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 15 | 30 | 15 | |
乙种品牌童装 | 球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 30 | 15 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
(x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】运动员将小球沿与地面成一定角度的方向击出,在不考虑空气阻力的条件下,小球的飞行高度h(m)与它的飞行时间t(s)满足二次函数关系,t与h的几组对应值如下表所示.
t(s) | 0 | 0.5 | 1 | 1.5 | 2 | … |
h(m) | 0 | 8.75 | 15 | 18.75 | 20 | … |
(1)求h与t之间的函数关系式(不要求写t的取值范围);
(2)求小球飞行3s时的高度;
(3)问:小球的飞行高度能否达到22m?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
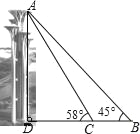
【题目】奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度(测角仪高度忽略不计).他们的操作方法如下:如图,他们先在B处测得最高塔塔顶A的仰角为45°,然后向最高塔的塔基直行90米到达C处,再次测得最高塔塔顶A的仰角为58°.请帮助他们计算出最高塔的高度AD约为多少米.(参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,抛物线y=ax2+bx+4![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点D,且3OC=4OB,对称轴为直线x=
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点D,且3OC=4OB,对称轴为直线x=![]() ,点E
,点E![]() ,连接CE交对称轴于点F,连接AF交抛物线于点G.
,连接CE交对称轴于点F,连接AF交抛物线于点G.
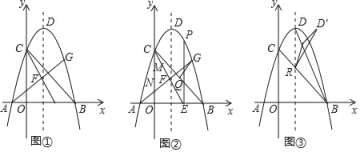
(1)求抛物线的解析式和直线CE的解析式;
(2)如图②,过E作EP⊥x轴交抛物线于点P,点Q是线段BC上一动点,当QG+![]() QB最小时,线段MN在线段CE上移动,点M在点N上方,且MN=
QB最小时,线段MN在线段CE上移动,点M在点N上方,且MN=![]() ,请求出四边形PQMN周长最小时点N的横坐标;
,请求出四边形PQMN周长最小时点N的横坐标;
(3)如图③,BC与对称轴交于点R,连接BD,点S是线段BD上一动点,将△DRS沿直线RS折叠至△D′RS,是否存在点S使得△D′RS与△BRS重叠部分的图形是直角三角形?若存在,请求出BS的长,若不存在,请说明理由.(参考数据:tan∠DBC=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
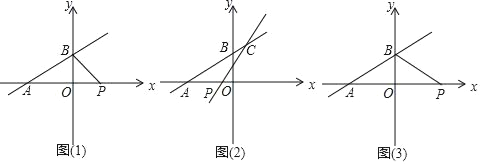
【题目】如图1,一次函数y=![]() x+4与x轴、y轴分别交于A,B两点.P是x轴上的动点,设点P的横坐标为n.
x+4与x轴、y轴分别交于A,B两点.P是x轴上的动点,设点P的横坐标为n.
(1)当△BPO∽△ABO时,求点P的坐标;
(2)如图2,过点P的直线y=2x+b与直线AB相交于C,求当△PAC的面积为20时,点P的坐标;
(3)如图3,直接写出当以A,B,P为顶点的三角形为等腰三角形时,点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com