
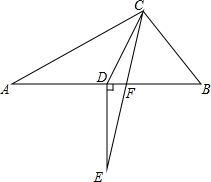
 已知:在△ABC中,∠ACB=90°,CF是∠ACB的交平分线,点D在边AB上,∠ACD=∠A,ED⊥AB交CF的延长线于点E,求证:∠E=∠DCF.
已知:在△ABC中,∠ACB=90°,CF是∠ACB的交平分线,点D在边AB上,∠ACD=∠A,ED⊥AB交CF的延长线于点E,求证:∠E=∠DCF. 分析 由∠ACB=90°,CF是∠ACB的交平分线,得到∠ACF=∠BCF=45°,于是得到∠DCF=45°-∠ACD=45°-∠A,根据三角形外角的性质得到∠AFC=45°+∠A,由ED⊥AB,得到∠E=90°-∠DFE,根据直角三角形的性质即可得到结论.
解答 证明:∵∠ACB=90°,CF是∠ACB的交平分线,
∴∠ACF=∠BCF=45°,
∵∠ACD=∠A,
∴∠DCF=45°-∠ACD=45°-∠A,
∴∠AFC=45°+∠A,
∵ED⊥AB,
∴∠E=90°-∠DFE,
∵∠DFE=∠CFB,
∴∠E=90°-(45°+∠A)=45°-∠A,
∴∠E=∠DCF.
点评 本题考查了三角形的内角和,角平分线的定义,直角三角形的性质,三角形外角的性质,熟练掌握各性质定理是解题的关键.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:填空题
 如图是某年11月份的日历,现用一长方形虚框在日历中任意框出4个数
如图是某年11月份的日历,现用一长方形虚框在日历中任意框出4个数 ,如果a+c=n(n是符合日历中数值条件的整数),那么用只含n的代数式表示b+d的值为n+2.
,如果a+c=n(n是符合日历中数值条件的整数),那么用只含n的代数式表示b+d的值为n+2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com