
【题目】某商场将某种商品的售价从原来的每件![]() 元经两次调价后调至每件
元经两次调价后调至每件![]() 元.
元.
(1)若该商店两次调价的降价率相同,求这个降价率;
(2)经调查,该商品每降价![]() 元,即可多销售
元,即可多销售![]() 件.若该商品原来每月可销售
件.若该商品原来每月可销售![]() 件,那么两次调价后,每月可销售该商品多少件?
件,那么两次调价后,每月可销售该商品多少件?
 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有_____名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为_____;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.
(1)求抛物线的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图象的函数关系式;
(3)设(2)中平移后,所得抛物线与y轴的交点为B1,顶点为D1,若点N在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
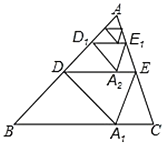
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第1次操作,折痕
处,称为第1次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,还原纸片后,再将
,还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第2次操作,折痕
处,称为第2次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,按上述方法不断操作下去…经过第2020次操作后得到的折痕
,按上述方法不断操作下去…经过第2020次操作后得到的折痕![]() 到
到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点, ![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由7个同样大小的正方体摆成的几何体.将正方体①移走后,所得几何体( )
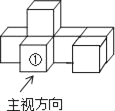
A. 主视图改变,俯视图改变 B. 左视图改变,俯视图改变
C. 俯视图不变,左视图改变 D. 主视图不变,左视图不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若四边形中某个顶点与其它三个顶点的距离相等,则这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.
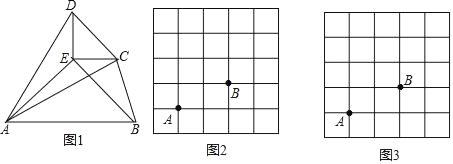
(1)判断:一个内角为120°的菱形 等距四边形.(填“是”或“不是”)
(2)如图2,在5×5的网格图中有A、B两点,请在答题卷给出的两个网格图上各找出C、D两个格点,使得以A、B、C、D为顶点的四边形为互不全等的“等距四边形”,画出相应的“等距四边形”,并写出该等距四边形的端点均为非等距点的对角线长.端点均为非等距点的对角线长为 端点均为非等距点的对角线长为
(3)如图1,已知△ABE与△CDE都是等腰直角三角形,∠AEB=∠DEC=90°,连结AD,AC,BC,若四边形ABCD是以A为等距点的等距四边形,求∠BCD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=( )

A.1.2 里B.1.5 里C.1.05 里D.1.02 里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com