
【题目】已知:如图,在平面直角坐标系中,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
![]() 求
求![]() 的长;
的长;
![]() 过点
过点![]() 作
作![]() ,交轴于点
,交轴于点![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 在
在![]() 的条件下,如果
的条件下,如果![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,连接
上的动点,连接![]() ,设
,设![]() ,问是否存在这样的使得
,问是否存在这样的使得![]() 与
与![]() 相似?若存在,请求出的
相似?若存在,请求出的![]() 值;若不存在,请说明理由.
值;若不存在,请说明理由.

【答案】![]() 的长为
的长为![]() ;
;![]() 的坐标为
的坐标为![]() ;
;![]() 存在,
存在,![]() 的值为
的值为![]() 或
或![]() .
.
【解析】
(1)根据点A、B的坐标分别为A(-4,0),B(0,3)可知OB=3,AO=4,利用勾股定理即可求出AB.
(2)根据BC⊥AB,BO⊥AC,利用射影定理即可求出OC,然后可知C点的坐标.
(3)假设△APQ与∽△ABC,利用其对应边成比例即可求出x的值.
(1)∵点A.B的坐标分别为A(4,0),B(0,3),
∴OB=3,AO=4,
∴![]()
(2)∵BC⊥AB,BO⊥AC,
∴![]() 即
即![]()
∴C点的坐标是(2.25,0);
(3)
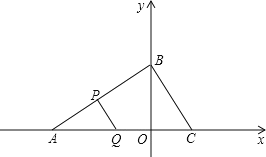
当△APQ与∽△ABC时,PQ∥BC,
∴![]()
∵AP=CQ=x,
∴![]()
解得![]()
当△APQ与∽△ACB时,![]()
即![]()
解得:![]() .
.
答:(1)AB的长为5;(2)C的坐标为(2.25,0);(3)存在,x的值为![]() 或
或![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其他区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1 000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,直线![]() 分别交
分别交![]() 轴
轴![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 的长满足
的长满足![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() .
.

![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 求过点
求过点![]() 的反比例函数解析式;
的反比例函数解析式;
![]() 点
点![]() 在反比例函数图象上是否存在一点
在反比例函数图象上是否存在一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点,
为顶点,![]() 为腰的四边形为梯形?若存在,请直接写出点
为腰的四边形为梯形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后回答问题 .
已知 ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,….,当
,….,当![]() 为大于1的奇数时,
为大于1的奇数时,![]() ;当
;当![]() 为大于1的偶数时,
为大于1的偶数时,![]() .
.
(1)求![]() ;(用含
;(用含![]() 的代数式表示)
的代数式表示)
(2)直接写出![]() ;(用含
;(用含![]() 的代数式表示)
的代数式表示)
(3)计算:![]() = .
= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,是瑞安部分街道示意图,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为“公交汽车”停靠点,甲公共汽车从
为“公交汽车”停靠点,甲公共汽车从![]() 站出发,按照
站出发,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的顺序到达
的顺序到达![]() 站,乙公共汽车从
站,乙公共汽车从![]() 站出发,按照
站出发,按照![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的顺序到达
的顺序到达![]() 站,如果甲、乙两车分别从
站,如果甲、乙两车分别从![]() 、
、![]() 两站同时出发,各站耽误的时间相同,两辆车速度也一样,则( )
两站同时出发,各站耽误的时间相同,两辆车速度也一样,则( )
A. 甲车先到达指定站 B. 乙车先到达指定站
C. 同时到达指定站 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,D是AB边上一点(点D与A,B不重合),连接CD,过点C作CE⊥CD,且CE=CD,连接DE交BC于点F,连接BE.
(1)求证:AB⊥BE;
(2)当AD=BF时,求∠BEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
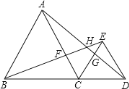
【题目】如图,将△ABC分别沿AB,AC翻折得到△ABD 和△AEC,线段BD与AE交于点 F,连接BE .
(1)如果∠ABC=16,∠ACB=30°,求∠DAE的度数;
(2)如果BD⊥CE,求∠CAB 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】建立模型:
如图1,等腰Rt△ABC中,∠ABC=90°,CB=BA,直线ED经过点B,过A作AD⊥ED于D,过C作CE⊥ED于E.则易证△ADB≌△BEC.这个模型我们称之为“一线三垂直”.它可以把倾斜的线段AB和直角∠ABC转化为横平竖直的线段和直角,所以在平面直角坐标系中被大量使用.

模型应用:
(1)如图2,点A(0,4),点B(3,0),△ABC是等腰直角三角形.
①若∠ABC=90°,且点C在第一象限,求点C的坐标;
②若AB为直角边,求点C的坐标;
(2)如图3,长方形MFNO,O为坐标原点,F的坐标为(8,6),M、N分别在坐标轴上,P是线段NF上动点,设PN=n,已知点G在第一象限,且是直线y=2x一6上的一点,若△MPG是以G为直角顶点的等腰直角三角形,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是甲乙两个工程队完成某项工程的进度图,首先是甲独做了10天,然后两队合做,完成剩下的工程.

(1)甲队单独完成这项工程,需要多少天?
(2)求乙队单独完成这项工程需要的天数;
(3)实际完成的时间比甲独做所需的时间提前多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com