
【题目】如图①,点P是正方形ABCD的BC边上的一点,以DP为边长的正方形DEFP与正方形ABCD在BC的同侧,连接AC,FB.
(1)请你判断FB与AC又怎样的位置关系?并证明你的结论;
(2)若点P在射线CB上运动时,如图②,判断(1)中的结论FB与AC的位置关系是否仍然成立?并说明理由;
(3)当点P在射线CB上运动时,请你指出点E的运动路线,不必说明理由.
【答案】
(1)FB∥AC,
证明:过F作FM⊥BC于M,
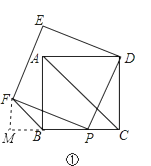
∵四边形ABCD、DEFP是正方形,
∴∠ACB=45°,DC=BC,PF=DP,∠DCP=∠M=∠FPD=90°,
∴∠MFP+∠FPM=∠FPM+∠DPC=90°,
∴∠MFP=∠CPD,
在△PFM和△DPC中

∴△PFM≌△DPC(AAS),
∵DC=PM,FM=PC,
∵DC=BC,
∴BC=DC=PM,
∴PM﹣BP=BC﹣BP,
∴BM=CP,
∵FM=CP,
∴FM=BM,
∵∠M=90°,
∴∠FBM=∠MFB= ![]() (180°﹣90°)=45°,
(180°﹣90°)=45°,
∵∠ACB=45°,
∴∠ACB=∠FBM,
∴FB∥AC
(2)解:结论仍成立,
理由是:过F作FM⊥BC于M,
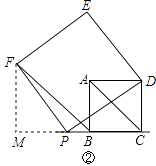
∵四边形ABCD、DEFP是正方形,
∴∠ACB=45°,DC=BC,PF=DP,∠DCP=∠M=∠FPD=90°,
∴∠MFP+∠FPM=∠FPM+∠DPC=90°,
∴∠MFP=∠CPD,
在△PFM和△DPC中,
 ,
,
∴△PFM≌△DPC(AAS),
∵DC=PM,FM=PC,
∵DC=BC,
∴BC=DC=PM,
∴PM+BP=BC+BP,
∴BM=CP,
∵FM=CP,
∴FM=BM,
∵∠M=90°,
∴∠FBM=∠MFB= ![]() (180°﹣90°)=45°,
(180°﹣90°)=45°,
∵∠ACB=45°,
∴∠ACB=∠FBM,
∴FB∥AC
(3)解:当点P在直线BC上移动时,E的轨迹是图中的线段GA.
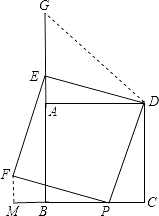
【解析】(1)通过观察可知二者平行,须延长CB连接MB构造全等三角形△PFM≌△DPC,得出内错角相等,即∠ACB=∠FBM,证得平行;(2)借鉴(1)的思路方法,辅助线仍和原来一样;(3)借鉴(1)(2)的图形,观察图1、2,E点始终在A的正上方,再寻找起始点,结束点,可确定是线段GA.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:
【题目】如图 1,直线![]() 分别交
分别交![]() 于点
于点![]() (点
(点![]() 在点
在点![]() 的右侧),若
的右侧),若![]()
(1)求证:![]() ;
;

(2)如图2所示,点![]() 在
在![]() 之间,且位于
之间,且位于![]() 的异侧,连
的异侧,连![]() , 若
, 若![]() ,则
,则![]() 三个角之间存在何种数量关系,并说明理由.
三个角之间存在何种数量关系,并说明理由.

(3)如图 3 所示,点![]() 在线段
在线段![]() 上,点
上,点![]() 在直线
在直线![]() 的下方,点
的下方,点![]() 是直线
是直线![]() 上一点(在
上一点(在![]() 的左侧),连接
的左侧),连接![]() ,若
,若![]() ,则请直接写出
,则请直接写出![]() 与
与![]() 之间的数量
之间的数量

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点P在线段AB外,且PA=PB,求证:点P在线段AB的垂直平分线上,在证明该结论时,需添加辅助线,则作法不正确的是( )

A. 作∠APB的平分线PC交AB于点C
B. 过点P作PC⊥AB于点C且AC=BC
C. 取AB中点C,连接PC
D. 过点P作PC⊥AB,垂足为C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD的对角线AC、BD相交于点O,OB=OD,BF=DE,AE∥CF.

(1)求证:△OAE≌△OCF;
(2)若OA=OD,猜想:四边形ABCD的形状,请证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF= ![]() CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.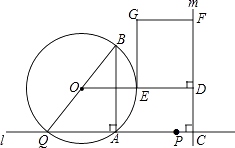
(1)用关于x的代数式表示BQ,DF.
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.
(3)在点P的整个运动过程中,
①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com