

分析 (1)连接OC,由AB为⊙O的直径,AB=2AC,得到△AOC是等边三角形,根据等边三角形的性质得到∠AOC=60°,于是得到结论;
(2)连接AE,OC与AE相交于F,由MC是⊙O的切线,得到MC⊥OC,求得∠MCO=∠CDB=90°,根据爬长城的判定定理得到BD∥OC,由平行线的性质得到∠AFO=∠AEB,由AB为⊙O的直径,得到∠AEB=90°,由垂径定理得到$\widehat{CE}=\widehat{AC}$,于是得到结论.
解答 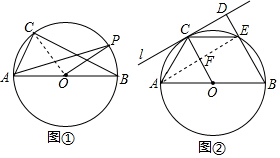 解:(1)连接OC,
解:(1)连接OC,
∵AB为⊙O的直径,AB=2AC,
∴OA=OC=AC,
∴△AOC是等边三角形,
∴∠AOC=60°,
∴∠APC=$\frac{1}{2}∠$AOC=30°;
(2)连接AE,OC与AE相交于F,
∵MC是⊙O的切线,
∴MC⊥OC,
∵BD⊥MC,
∴∠MCO=∠CDB=90°,
∴BD∥OC,
∴∠AFO=∠AEB,
∵AB为⊙O的直径,
∴∠AEB=90°,
∴∠AFO=90°,
∴OC⊥AE,
∴$\widehat{CE}=\widehat{AC}$,
∴CE=AC=$\frac{1}{2}$AB=$\frac{1}{2}×$4=2.
点评 本题考查了切线的性质,等边三角形的性质,垂径定理,平行线的判定和性质,正确的作出辅助线是解题的关键.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:解答题
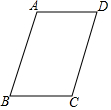 如图,四边形ABCD是平行四边形.
如图,四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
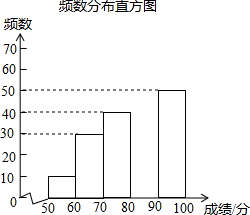 为了传承优秀传统文化,我县团委组织了一次全县有3000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
为了传承优秀传统文化,我县团委组织了一次全县有3000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:| 成绩x/分 | 频数 | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 40 | n |
| 80≤x<90 | m | 0.35 |
| 90≤x≤100 | 50 | 0.25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
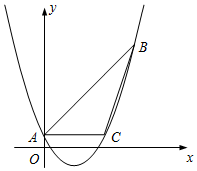 如图,已知抛物线y=ax2-2x+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴.
如图,已知抛物线y=ax2-2x+c经过△ABC的三个顶点,其中点A(0,1),点B(9,10),AC∥x轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
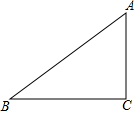 如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°,若点A,B的对应点分别是点D,E.
如图,在△ABC中,∠ACB=90°,AB=5,BC=4,将△ABC绕点C顺时针旋转90°,若点A,B的对应点分别是点D,E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -5 | -4 | -3 | -2 | -1 | … |
| y | … | -7.5 | -2.5 | 0.5 | 1.5 | 0.5 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com