
如图,已知AB∥CD,∠AEC=90°,那么∠A与∠C的度数和为多少度?为什么?
解:∠A与∠C的度数和为 _________ .
理由:过点E作EF∥AB,
∵EF∥AB,
∴∠A+∠AEF=180°( _________ ).
∵AB∥CD( _________ ),EF∥AB,
∴EF∥CD( _________ )
∴ _________ (两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C= _________ °(等式的性质)
即∠A+∠AEC+∠C= _________ °
∵∠AEC=90°(已知)
∴∠A+∠C= _________ °(等式的性质).
270°,完成理由证明见解析.
解析试题分析:
关键是过点E作EF∥AB,
则利用两直线平行,同旁内角互补。得∠A+∠AEF=180°
再有AB∥CD和 EF∥AB,可知EF∥CD
由两直线平行,同旁内角互补,得到∠C+∠CEF=180°
则得到∠A+∠AEF+∠CEF+∠C=360°,据等式的性质 即∠A+∠AEC+∠C=360°
又∠AEC=90°得到∠A+∠C=270°.
试题解析:∠A与∠C的度数和为 270°.
理由:过点E作EF∥AB,
∵EF∥AB,
∴∠A+∠AEF=180°(两直线平行,同旁内角互补).
∵AB∥CD( 已知 ),EF∥AB,
∴EF∥CD(平行于同一条直线的两条直线互相平行)
∴∠C+∠CEF=180°(两直线平行,同旁内角互补)
∴∠A+∠AEF+∠CEF+∠C= 360°(等式的性质)
即∠A+∠AEC+∠C= 360°°
∵∠AEC=90°(已知)
∴∠A+∠C= 270°(等式的性质).
考点:两直线平行,同旁内角互补.


科目:初中数学 来源: 题型:解答题
已知AB∥CD,分别探讨下列四个图形中∠APC和∠A、∠C的关系,并选择图(1)、(2)之一说明理由。 (10分)
(1) (2) (3) (4)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:如图,EF⊥AB,CD⊥AB,AC⊥BC,∠1=∠2,求证:DG⊥BC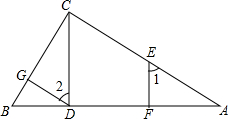
证明:∵EF⊥AB CD⊥AB
∴∠EFA=∠CDA=90°(垂直定义)
∠1=∠
∴EF∥CD
∴∠1=∠2(已知)
∴∠2=∠ACD(等量代换)
∴DG∥AC
∴∠DGB=∠ACB
∵AC⊥BC(已知)
∴∠ACB=90°(垂直定义)
∴∠DGB=90°即DG⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于 CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是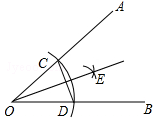
A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.C、D两点关于OE所在直线对称
D.O、E两点关于CD所在直线对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com