练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．先化简，再求值：$（1+\frac{3}{a-2}）÷\frac{{{a^2}-1}}{a-2}$，其中a=$\sqrt{5}$+1．

    分析 原式去括号、化除法为乘法，进行约分，得到最简结果，把a的值代入计算即可求出值．

    解答 解：原式=$\frac{a-2+3}{a-2}$•$\frac{a-2}{（a+1）（a-1）}$
    =$\frac{1}{a-1}$，
    当a=$\sqrt{5}$+1时，
    原式=$\frac{1}{\sqrt{5}+1-1}$=$\frac{\sqrt{5}}{5}$．

    点评 本题考查了分式的化简求值．在化简的过程中要注意运算顺序和分式的化简．化简的最后结果分子、分母要进行约分，注意运算的结果要化成最简分式或整式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

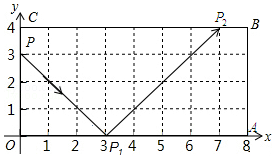    12．如图，弹性小球从点P（0，3）出发，沿所示方向运动，每当小球碰到矩形OABC的边时反弹，反弹时反射角等于入射角，当小球第1次碰到矩形的边时，记为点P1，第2次碰到矩形的边时，记为点P2，…第n次碰到矩形的边时，记为点Pn，则点P3的坐标是（8，3）；点P2017的坐标是（3，0）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．一只不透明的袋子中装有1个红球、2个绿球和3个白球，每个球除颜色外都相同．将球搅匀后，从中任意摸出一球．
    （1）会有哪些等可能的结果；
    （2）你认为摸到哪种颜色的球可能性最大？摸到哪种颜色的球可能性最小？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．（1）如图1，四边形ABCD是正方形，点E、点F分别在边AB和AD上，且AE=AF．此时，线段BE、DF的数量关系是BE=DF，位置关系是BE⊥DF．请直接写出结论．
    （2）如图2，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当0°＜α＜90°时，连接BE、DF，此时（1）中的结论是否成立，如果成立，请证明；如果不成立，请说明理由．
    （3）如图3，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当α=90°时，连接BE、DF，若正方形的边长为1，猜想当AE=$\sqrt{2}$-1时，直线DF垂直平分BE．请写出计算过程．
    （4）如图4，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当90°＜α＜180°时，连接BD、DE、EF、FB得到四边形BDEF，则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形？请直接写出结论：正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．已知y=$\sqrt{2x-5}$+$\sqrt{5-2x}$-3，则xy的值为-$\frac{15}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算或化简
    （1）（-1）3+$\sqrt{8}$-|1-$\sqrt{2}$|
    （2）$\sqrt{48}$÷$\sqrt{3}$-$\sqrt{\frac{1}{2}}$×$\sqrt{12}$+$\sqrt{24}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．某地区住宅用电之电费计算规则如下：每月每户不超过50度时，每度以4元收费；超过50度的部分，每度以5元收费，并规定用电按整数度计算（小数部份无条件舍去）．
    （1）下表给出了今年3月份A，B两用户的部分用电数据，请将表格数据补充完整，
    电量（度）电费（元）
    A58240
    B32128
    合计90368
    （2）若假定某月份C用户比D用户多缴电费38元，求C用户该月可能缴的电费为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图1，△ABC中，AB=AC，∠C=60°，D、E分别在BC、AC上，CD=AE．
    （1）如图1，连BE、AD，求证：AE2=EF•EB；
    （2）如图2，过E点作EG∥CF交AD于G点，求证：BF=DG．
    （3）如图3，若BD=2CD，求证：BF⊥CF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图是“赵爽弦图”，其中△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABC的和EFGH都是正方形．根据这个图形的面积关系，可以证明勾股定理．设AD=c，AE=b，c=10，a-b=2．
    （1）正方形EFGH的面积为4，四个直角三角形的面积和为96．
    （2）求（a+b）2的值．
    （3）a+b=14，a=8，b=6．

    查看答案和解析>>

    同步练习册答案