
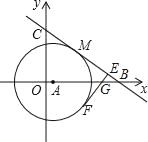
【题目】如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=﹣![]() x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
(1)直接写出b的值和点B的坐标;
(2)求点A的坐标和圆的半径;
(3)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求![]() 的值.
的值.
【答案】(1)y=﹣![]() x+7;B(
x+7;B(![]() ,0)(2)圆A的半径为5(3)3
,0)(2)圆A的半径为5(3)3
【解析】试题分析:(1)将点M的坐标代入直线![]() 的解析式可求得b的值,由b的值可得到直线的解析式,然后令y=0可求得点B的横坐标,于是得到点B的坐标;
的解析式可求得b的值,由b的值可得到直线的解析式,然后令y=0可求得点B的横坐标,于是得到点B的坐标;
(2)由相互垂直的两条直线的一次项系数为-1,可设直线AM的解析式为![]()
然后将点M的坐标代入可求得c的值,然后令y=0可求得点A的横坐标,最后依据两点间的距离公式可求得圆A的半径.
(3)如图1所示:连接AF、AM.先证明四边形AFEM为正方形,于是可求得ME=5,然后在△ABM中依据勾股定理可求得MB的长,从而可求得BE的长,接下来,证明![]() 由相似三角形的性质可求得答案.
由相似三角形的性质可求得答案.
试题解析:
(1)∵点M在直线![]() 上,
上,
![]() 解得:b=7.
解得:b=7.
∴直线的解析式为![]()
∵当y=0时, ![]() ,解得:
,解得: ![]()
![]()
(2)∵BC是圆A的切线,
∴AM⊥BC.
设直线AM的解析式为![]()
∵将M(4,4)代入![]() 得
得![]() 解得:
解得: ![]()
∴直线AM的解析式为![]()
∵当y=0时, ![]() 解得x=1,
解得x=1,
∴A(1,0).
∵由两点间的距离公式可知![]()
∴圆A的半径为5.
(3)如图1所示:连接AF、AM.
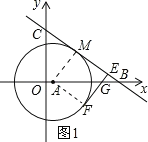
∵BC、EF是圆A的切线,
∴AM⊥BC,AF⊥EF.
又∵BC⊥EF,
![]()
∴四边形AFEM为矩形,
又∵AM=AF,
∴四边形AFEM为正方形,
∴ME=AF=5.
∵在Rt△AMB中, ![]()
![]()
![]()
∴△AGF∽△BGE.
![]() 即
即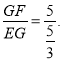
![]()


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
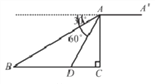
【题目】如图,某无人机于空中A处探测到目标B、D的俯角分别是30°、60°,此时无人机的飞行高度AC为60m.随后无人机从A处继续水平飞行30![]() m到达A′处.
m到达A′处.
(1)求A、B之间的距离:
(2)求从无人机A′上看目标D的俯角的正切值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从相距480km的A.B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途径C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
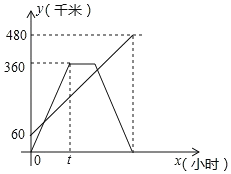
(1)乙车的速度是___千米/时,t=___小时;
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围;
(3)直接写出两车相距150千米时x的取值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于受到手机更新换代的影响,某手机店经销的甲型号手机二月份售价比一月份售价每台降价500元.如果卖出相同数量的手机,那么一月份销售额为9万元,二月份销售额只有8万元.
(1)求二月份甲型号手机每台售价为多少元?
(2)为了提高利润,该店计划三月份加入乙型号手机销售,已知甲型每台进价为3500元,乙型每台进价为4000元,预计用不多于7.6万元且不少于7.5万元的资金购进这两种手机共20台,请问有几种进货方案?
(3)对于(2)中刚进货的20台两种型号的手机,该店计划对甲型号手机在二月份售价基础上每售出一台甲型手机再返还顾客现金a元,乙型手机按销售价4400元销售,若要使(2)中所有方案获利相同,a应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为建设美丽农村,村委会打算在正方形地块甲和长方形地块乙上进行绿化.在两地块内分别建造一个边长为![]() 的大正方形花坛和四个边长为
的大正方形花坛和四个边长为![]() 的小正方形花坛(阴影部分),空白区域铺设草坪,记
的小正方形花坛(阴影部分),空白区域铺设草坪,记![]() 表示地块甲中空白处铺设草坪的面积,
表示地块甲中空白处铺设草坪的面积, ![]() 表示地块乙中空白处铺设草坪的面积.
表示地块乙中空白处铺设草坪的面积.

(1)![]() __ ,
__ ,![]() (用含
(用含![]() 的代数式表示并化简) .
的代数式表示并化简) .
(2)若![]() ,求
,求![]() 的值.
的值.
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=EF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知E、F分别为正方形ABCD的边BC、CD上的点,且∠EAF=45°.
(1)如图①求证:BE+DF=EF;
(2)连接BD分别交AE、AF于M、N,
①如图②,若AB=6![]() ,BM=3,求MN.
,BM=3,求MN.
②如图③,若EF∥BD,求证:MN=CE.
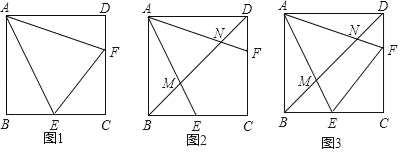
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=105°,∠DBC=75°.
(1)求证:BD=CD;
(2)若圆O的半径为3,求![]() 的长.
的长.
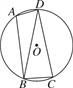
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com