
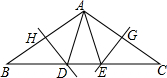
 如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )
如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( )| A. | $\frac{BD}{BC}$=$\frac{\sqrt{5}-1}{2}$ | B. | AD,AE将∠BAC三等分 | ||
| C. | △ABE≌△ACD | D. | S△ADH=S△CEG |
分析 由题意知AB=AC、∠BAC=108°,根据中垂线性质得∠B=∠DAB=∠C=∠CAE=36°,从而知△BDA∽△BAC,得$\frac{BD}{BA}$=$\frac{BA}{BC}$,由∠ADC=∠DAC=72°得CD=CA=BA,进而根据黄金分割定义知$\frac{BD}{BA}$=$\frac{BA}{BC}$=$\frac{\sqrt{5}-1}{2}$,可判断A;根据∠DAB=∠CAE=36°知∠DAE=36°可判断B;根据∠BAD+∠DAE=∠CAE+∠DAE=72°可得∠BAE=∠CAD,可证△BAE≌△CAD,即可判断C;由△BAE≌△CAD知S△BAD=S△CAE,根据DH垂直平分AB,EG垂直平分AC可得S△ADH=S△CEG,可判断D.
解答 解:∵∠B=∠C=36°,
∴AB=AC,∠BAC=108°,
∵DH垂直平分AB,EG垂直平分AC,
∴DB=DA,EA=EC,
∴∠B=∠DAB=∠C=∠CAE=36°,
∴△BDA∽△BAC,
∴$\frac{BD}{BA}$=$\frac{BA}{BC}$,
又∵∠ADC=∠B+∠BAD=72°,∠DAC=∠BAC-∠BAD=72°,
∴∠ADC=∠DAC,
∴CD=CA=BA,
∴BD=BC-CD=BC-AB,
则$\frac{BC-BA}{BA}=\frac{BA}{BC}$=$\frac{\sqrt{5}-1}{2}$,即$\frac{BD}{BA}$=$\frac{BA}{BC}$=$\frac{\sqrt{5}-1}{2}$,故A错误;
∵∠BAC=108°,∠B=∠DAB=∠C=∠CAE=36°,
∴∠DAE=∠BAC-∠DAB-∠CAE=36°,
即∠DAB=∠DAE=∠CAE=36°,
∴AD,AE将∠BAC三等分,故B正确;
∵∠BAE=∠BAD+∠DAE=72°,∠CAD=∠CAE+∠DAE=72°,
∴∠BAE=∠CAD,
在△BAE和△CAD中,
∵$\left\{\begin{array}{l}{∠B=∠C}\\{AB=AC}\\{∠BAE=∠CAD}\end{array}\right.$,
∴△BAE≌△CAD,故C正确;
由△BAE≌△CAD可得S△BAE=S△CAD,即S△BAD+S△ADE=S△CAE+S△ADE,
∴S△BAD=S△CAE,
又∵DH垂直平分AB,EG垂直平分AC,
∴S△ADH=$\frac{1}{2}$S△ABD,S△CEG=$\frac{1}{2}$S△CAE,
∴S△ADH=S△CEG,故D正确.
故选:A.
点评 本题主要考查黄金分割、全等三角形的判定与性质及线段的垂直平分线的综合运用,掌握其性质、判定并灵活应用是解题的关键.


科目:初中数学 来源: 题型:解答题
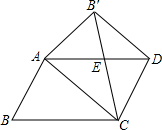 我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.
我们知道平行四边形有很多性质,现在如果我们把平行四边形沿着它的一条对角线翻折,会发现这其中还有更多的结论.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )
如图,在Rt△ABC中,∠A=30°,BC=1,点D,E分别是直角边BC,AC的中点,则DE的长为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 1+$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 8 | C. | 2或8 | D. | 2<O1O2<8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
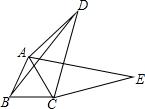 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.
如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形.线段CD绕点C顺时针旋转60°得到线段CE,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
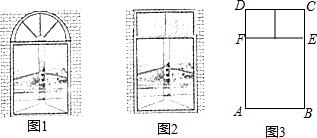
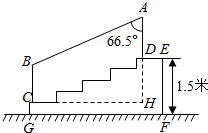 如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)
如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7.6×10-9 | B. | 7.6×10-8 | C. | 7.6×109 | D. | 7.6×108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com