
【题目】如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为(4,0),点B的坐标为(0,1),点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE.
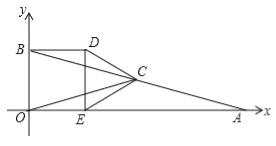
(1)线段OC的长为 ;
(2)求证:△CBD≌△COE;
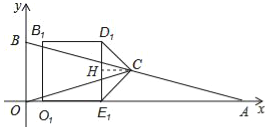
(3)将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1,其中点O,B,D,E的对应点分别为点O1,B1,D1,E1,连接CD,CE,设点E的坐标为(a,0),其中a≠2,△CD1E1的面积为S.
①当1<a<2时,请直接写出S与a之间的函数表达式;
②在平移过程中,当S=![]() 时,请直接写出a的值.
时,请直接写出a的值.
【答案】(1)![]() ;(2)详见解析;(3)①S=﹣
;(2)详见解析;(3)①S=﹣![]() a+1;②当S=
a+1;②当S=![]() 时,a=
时,a=![]() 或
或![]() .
.
【解析】
试题分析:(1)由点A的坐标为(4,0),点B的坐标为(0,1),根据勾股定理求得AB的长,再由点C为边AB的中点,根据直角三角形斜边的中线等于斜边的一半,即可求得线段OC的长;(2)由四边形OBDE是正方形,直角三角形斜边的中线等于斜边的一半,易得BD=OE,BC=OC,∠CBD=∠COE,即可证得:△CBD≌△COE;(3)①首先根据题意画出图形,然后过点C作CH⊥D1E1于点H,可求得△CD1E1的高与底,继而求得答案;
②分别从1<a<2与a>2去分析求解即可求得答案.
试题解析:(1)∵点A的坐标为(4,0),点B的坐标为(0,1),
∴OA=4,OB=1,
∵∠AOB=90°,
∴AB=![]() ,
,
∵点C为边AB的中点,
∴OC=![]() AB=
AB=![]() ;
;
(2)证明:∵∠AOB=90°,点C是AB的中点,
∴OC=BC=![]() AB,
AB,
∴∠CBO=∠COB,
∵四边形OBDE是正方形,
∴BD=OE,∠DBO=∠EOB=90°,
∴∠CBD=∠COE,
在△CBD和△COE中,
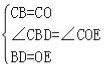 ,
,
∴△CBD≌△COE(SAS);
(3)①解:过点C作CH⊥D1E1于点H,
∵C是AB边的中点,
∴点C的坐标为:(2,![]() )
)
∵点E的坐标为(a,0),1<a<2,
∴CH=2﹣a,
∴S=![]() D1E1CH=
D1E1CH=![]() ×1×(2﹣a)=﹣
×1×(2﹣a)=﹣![]() a+1;
a+1;
②当1<a<2时,S=﹣![]() a+1=
a+1=![]() ,
,
解得:a=![]() ;
;
当a>2时,同理:CH=a﹣2,
∴S=![]() D1E1CH=
D1E1CH=![]() ×1
×1![]() a﹣1,
a﹣1,
∴S=![]() a﹣1=
a﹣1=![]() ,
,
解得:a=![]() ,
,
综上可得:当S=![]() 时,a=
时,a=![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】下列调查适合作普查的是 ( ).
A. 了解在校大学生的主要娱乐方式
B. 了解某市居民对废电池的处理情况
C. 日光灯管厂要检测一批灯管的使用寿命
D. 对甲型H7N9流感患者的同一车厢的乘客进行医学检查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
A.32,31
B.31,32
C.31,31
D.32,35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了传承优秀传统文化,某校开展“经典诵读”比赛活动,诵读材料有《论语》,《三字经》,《弟子规》(分别用字母A,B,C依次表示这三个诵读材料),将A,B,C这三个字母分别写在3张完全相同的不透明卡片的正面上,把这3张卡片背面朝上洗匀后放在桌面上.小明和小亮参加诵读比赛,比赛时小明先从中随机抽取一张卡片,记录下卡片上的内容,放回后洗匀,再由小亮从中随机抽取一张卡片,选手按各自抽取的卡片上的内容进行诵读比赛.
(1)小明诵读《论语》的概率是 .
(2)请用列表法或画树状图法求小明和小亮诵读两个不同材料的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y=![]() 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=
的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
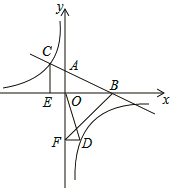
(1)求反比例函数的解析式;
(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF,如果S△BAF=4S△DFO,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com