
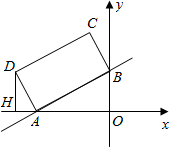
��֪����ƽ��ֱ������ϵxOy�У�һ�κ���![]() ��ͼ����x�ύ�ڵ�A��������
��ͼ����x�ύ�ڵ�A��������![]() ����O��A���㡣
����O��A���㡣
��1�����ú�a�Ĵ���ʽ��ʾb��
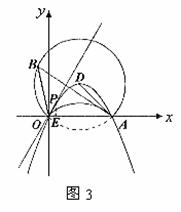
��2���������ߵĶ���ΪD����DΪԲ�ģ�DAΪ�뾶��Բ��x���Ϊ�ӻ����Ż������֡������ӻ���x�ᷭ�ۣ����ۺ���ӻ����ڡ�D�ڣ������ڵ�Բǡ��OD���У����D�뾶�ij��������ߵĽ���ʽ��
��3�����B�����㣨2�����������Ż��ϵ�һ�����㣬��������x���Ϸ��IJ������Ƿ���������ĵ�P��ʹ��![]() �������ڣ������P�����ꣻ�������ڣ���˵�����ɡ�
�������ڣ������P�����ꣻ�������ڣ���˵�����ɡ�
��1���ⷨһ����һ�κ���![]() ��ͼ����x�ύ�ڵ�A
��ͼ����x�ύ�ڵ�A
���A��������4��0�� ��������![]() ����O��A����
����O��A����
![]()
![]()
�ⷨ������һ�κ���![]() ��ͼ����x�ύ�ڵ�A
��ͼ����x�ύ�ڵ�A
���A��������4��0�� ��������![]() ����O��A����
����O��A����
�������ߵĶԳ���Ϊֱ��![]()
![]()
![]()
��2���⣺�������ߵĶԳ��Կ�֪��DO��DA ���O�ڡ�D�ϣ��ҡ�DOA����DAO
���ɣ�1��֪�����ߵĽ���ʽΪ![]() ���D������Ϊ��
���D��������![]() ��
��
�ٵ�![]() ʱ��
ʱ��
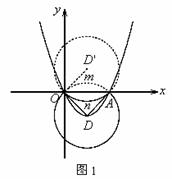
��ͼ1�����D��x��ֵõ��ӻ�Ϊ![]() ������x�ᷭ�ۺ������ӻ�Ϊ
������x�ᷭ�ۺ������ӻ�Ϊ![]() ����Ȼ
����Ȼ![]() ���ڵ�Բ���D����x��Գƣ�������Բ��ΪD'
���ڵ�Բ���D����x��Գƣ�������Բ��ΪD'
���D'���DҲ����x��Գ�
�ߵ�O�ڡ�D'�ϣ��ҡ�D���D'����
���OΪ�е�
��D'O��OD
���DOA����D'OA��45��
���ADOΪ����ֱ��������
![]()
���D��������Ϊ![]()
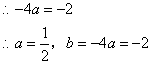
�������ߵĽ���ʽΪ![]()
�ڵ�![]() ʱ��
ʱ��
ͬ���ɵã�![]()
�����ߵĽ���ʽΪ![]()
���ϣ���D�뾶�ij�Ϊ![]() �������ߵĽ���ʽΪ
�������ߵĽ���ʽΪ![]() ��
��![]()
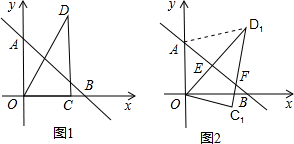
��3�������������x���Ϸ��IJ����ϴ��ڵ�P��ʹ��![]()
���P��������x��y������y��0
�ٵ���P��������![]() ��ʱ����ͼ2��
��ʱ����ͼ2��
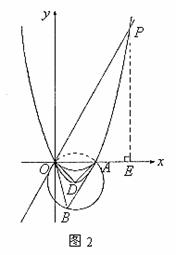
�ߵ�B�ǡ�D���Ż��ϵ�һ��
![]()
![]()
����P��PE��x���ڵ�E
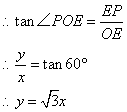
�� ��ã�
��ã� ����ȥ��
����ȥ��
���P������Ϊ![]()
�ڵ���P��������![]() ��ʱ����ͼ3��
��ʱ����ͼ3��
ͬ���ɵã�![]()
��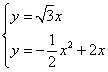 ��ã�
��ã�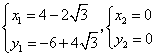 ����ȥ��
����ȥ��
���P������Ϊ![]()
���ϣ��������������ĵ�P����P������Ϊ
![]() ��
��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| k |
| x |
| 3 |
| x |
| k |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ�������У���ֱ֪��y=kx+b��ֱ��y=
��ͼ����ƽ��ֱ�������У���ֱ֪��y=kx+b��ֱ��y=| 1 |
| 2 |
| 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=| k |
| x |
| k |
| x |
| 6 |
| x |
| 6 |
| x |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com