

(1)求BF的长;
(2)求BR的长;
(3)求BQ的长;
(4)求PQ的长.
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省锡麟中学七年级下学期期中考试数学卷(带解析) 题型:解答题
在△ABC中,AB=AC,∠ACB =∠ABC,CG⊥BA交BA的延长线于点G,一等腰三角板按如图27-1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边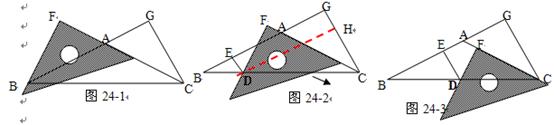
在一条直线上,另一条直角边恰好经过点B。
(1)在图24-1中请你通过观察,测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后说明你的猜想。
(2)当三角尺沿AC方向平移到图24-2所在的位置时,一条直角边仍与AC边在同一直线上,另
一条直角边交BC边于点D,过点D作DE⊥BA于点E,此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后说明你的猜想。
(提示:过点D作DH⊥CG,可得四边形EDHG是长方形,而且∠HDC=∠ABC,ED=GH)
(3)当三角尺在(2)的基础上沿AC方向继续平移到图24-3所示的位置(点F在线段AC上,
且点F与点C不重合)时,试猜想DE、DF与CG之间满足的数量关系?(不用说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
在△ABC中,AB=AC,∠ACB =∠ABC,CG⊥BA交BA的延长线于点G,一等腰三角板按如图27-1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边

在一条直线上,另一条直角边恰好经过点B。
(1)在图24-1中请你通过观察,测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后说明你的猜想。
(2)当三角尺沿AC方向平移到图24-2所在的位置时,一条直角边仍与AC边在同一直线上,另
一条直角边交BC边于点D,过点D作DE⊥BA于点E,此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后说明你的猜想。
(提示:过点D作DH⊥CG,可得四边形EDHG是长方形,而且∠HDC=∠ABC,ED=GH)
(3)当三角尺在(2)的基础上沿AC方向继续平移到图24-3所示的位置(点F在线段AC上,
且点F与点C不重合)时,试猜想DE、DF与CG之间满足的数量关系?(不用说明理由)
【解析】本题利用等腰直角三角形的性质及全等三角形的判定和性质求解
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com