
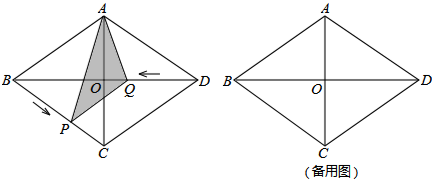
分析 (1)过点A作AH⊥CD于H,如图1.利用菱形的性质及勾股定理就可求出AB的值,然后运用菱形的面积公式就可求出AB与CD之间的距离;
(2)当0≤x≤5时,点P在BC上,如图2①、图2②.过点A作AE⊥BC于E,过点P作PG⊥BD于G,则有PG∥OC,从而可得△BGP∽△BOC,根据相似三角形的性质可得PG=$\frac{3}{5}$x,从而可用x的代数式表示出S△ABQ,S△PBQ,S△ABP,然后运用割补法就可解决问题;
(3)可分两种情况讨论(①PQ∥CD,②PQ∥BC),然后运用相似三角形的性质就可解决问题.
解答 解:(1)过点A作AH⊥CD于H,如图1.
∵四边形ABCD是菱形,
∴AO=OC=$\frac{1}{2}$AC=3,BO=DO=$\frac{1}{2}$BD=4,AB=BC=CD=AD,AC⊥BD,
∴AB=$\sqrt{A{O}^{2}+B{O}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∵S菱形ABCD=$\frac{1}{2}$AC•BD=CD•AH,
∴$\frac{1}{2}$×6×8=5AH,
∴AH=4.8.
故答案为5、4.8;
(2)当0≤x≤5时,点P在BC上,如图2①、图2②.

过点A作AE⊥BC于E,过点P作PG⊥BD于G,
则有PG∥OC,
∴△BGP∽△BOC,
∴$\frac{PG}{OC}$=$\frac{BP}{BC}$,即$\frac{PG}{3}$=$\frac{x}{5}$,∴PG=$\frac{3}{5}$x,
∴S△ABQ=$\frac{1}{2}$BQ•AO=$\frac{1}{2}$(8-x)•3=12-$\frac{3}{2}$x,
S△PBQ=$\frac{1}{2}$BQ•PG=$\frac{1}{2}$(8-x)•$\frac{3}{5}$x=$\frac{12}{5}$x-$\frac{3}{10}$x2,
S△ABP=$\frac{1}{2}$BP•AE=$\frac{1}{2}$x•$\frac{24}{5}$=$\frac{12}{5}$x,
∴y=|S△ABQ+S△PBQ-S△ABP|
=|12-$\frac{3}{2}$x+$\frac{12}{5}$x-$\frac{3}{10}$x2-$\frac{12}{5}$x|,
=|-$\frac{3}{10}$x2-$\frac{3}{2}$x+12|.
当y=0时,-$\frac{3}{10}$x2-$\frac{3}{2}$x+12=0,
整理得x2+5x-40=0,
解得x1=-$\frac{5}{2}$+$\frac{\sqrt{185}}{2}$,x2=-$\frac{5}{2}$-$\frac{\sqrt{185}}{2}$(舍负),
∴当0≤x≤-$\frac{5}{2}$+$\frac{\sqrt{185}}{2}$时,y=-$\frac{3}{10}$x2-$\frac{3}{2}$x+12;
当-$\frac{5}{2}$+$\frac{\sqrt{185}}{2}$<x≤5时,y=$\frac{3}{10}$x2+$\frac{3}{2}$x-12.
(3)符合条件的x的值为$\frac{40}{13}$、$\frac{80}{13}$.
提示:①当PQ∥CD时,如图3,
则有△BPQ∽△BCD,
∴$\frac{BP}{BC}$=$\frac{BQ}{BD}$,即$\frac{x}{5}$=$\frac{8-x}{8}$,
解得x=$\frac{40}{13}$;
②当PQ∥BC时,如图4,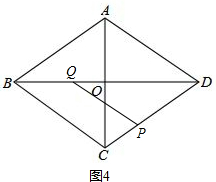
则有△DPQ∽△DCB,
∴$\frac{DQ}{DB}$=$\frac{DP}{DC}$,即$\frac{x}{8}$=$\frac{10-x}{5}$,
解得x=$\frac{80}{13}$.
点评 本题主要考查了相似三角形的判定与性质、菱形的性质、勾股定理、解一元二次方程、菱形的面积公式等知识,在解决问题的过程中,用到了分类讨论、割补法等重要的数学思想方法,应熟练掌握.需要注意的是,运用割补法求y与x的函数关系时,由于点A、P、Q三点共线前后,S△ABQ+S△PBQ与S△ABP的大小关系发生变化,故需分类讨论,避免出现漏解的现象.


科目:初中数学 来源: 题型:选择题
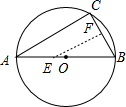 如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,(到点B终止远动)设运动时间为t(s),连结EF,当△BEF是直角三角形时,t(s)的值为( )
如图,AB是⊙O的直径,弦BC=2cm,F是弦BC的中点,∠ABC=60°.若动点E以2cm/s的速度从A点出发沿着A→B方向运动,(到点B终止远动)设运动时间为t(s),连结EF,当△BEF是直角三角形时,t(s)的值为( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 1或$\frac{7}{4}$ | D. | 1或$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
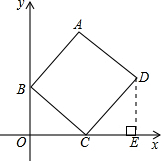 如图,在直角坐标系xOy内,四边形ABCD为正方形,已知点B(0,3),C(4,0).
如图,在直角坐标系xOy内,四边形ABCD为正方形,已知点B(0,3),C(4,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 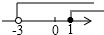 | B. | 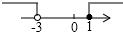 | C. |  | D. | 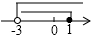 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
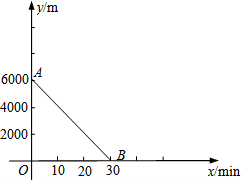 某日,小敏、小君两人约好去奥体中心打球.小敏13:00从家出发,匀速骑自行车前往奥体中心,小君13:05从离奥体中心6000m的家中匀速骑自行车出发.已知小君骑车的速度是小敏骑车速度的1.5倍.设小敏出发x min后,到达离奥体中心y m的地方,图中线段AB表示y与x之间的函数关系.
某日,小敏、小君两人约好去奥体中心打球.小敏13:00从家出发,匀速骑自行车前往奥体中心,小君13:05从离奥体中心6000m的家中匀速骑自行车出发.已知小君骑车的速度是小敏骑车速度的1.5倍.设小敏出发x min后,到达离奥体中心y m的地方,图中线段AB表示y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
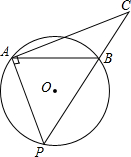 如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为8,$\frac{56}{15}$或$\frac{8\sqrt{5}}{3}$.
如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为8,$\frac{56}{15}$或$\frac{8\sqrt{5}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com