
分析 由条件可得DE为△ABC的中位线,可得DE∥BC,可得△ADE∽△ABC,且$\frac{DE}{BC}$=$\frac{1}{2}$,可得出S△ADE:S△ABC=1:4,从而可求得S△ADE:S梯形DBCE.
解答 解:∵D、E分别为AB、AC的中点,
∴DE∥BC,且$\frac{DE}{BC}$=$\frac{1}{2}$,
∴△ADE∽△ABC,
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=($\frac{DE}{BC}$)2=($\frac{1}{2}$)2=$\frac{1}{4}$,
∴$\frac{{S}_{△ADE}}{S梯形DEBC}$=$\frac{1}{3}$,
故答案为:1:3.
点评 本题主要考查相似三角形的判定和性质,利用条件得出S△ADE:S△ABC=1:4是解题的关键.


科目:初中数学 来源: 题型:解答题
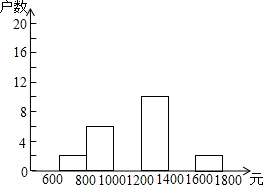 小龙在学校组织的社会调查活动中负责了解他所居住的小区480户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.
小龙在学校组织的社会调查活动中负责了解他所居住的小区480户居民的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.| 分组 | 频数 | 百分比 |
| 600≤x<800 | 2 | 5% |
| 800≤x<1000 | 6 | 15% |
| 1000≤x<1200 | a | 45% |
| 1200≤x<1400 | 9 | 22.5% |
| 1400≤x<1600 | b | c |
| 1600≤x<1800 | 2 | d |
| 合计 | 40 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com