
分析 (1)话费分两个阶梯缴纳,3分钟以内(包括3分钟)缴1.8元,超过3分钟的通话时间为(t-3)需多缴花费1.2(t-3)元;
(2)利用(1)所求的y与t的表达式求当t=2、当t=10是对应的y的值即可.
解答 解:(1)y=$\left\{\begin{array}{l}{1.8}&{(0<t≤3)}\\{1.8+1.2(t-3)}&{(t>3)}\end{array}\right.$
(2)①当t=2时,y=1.8
②当t=10时,y=1.8+1.2×(10-3)=1.8+8.4=10.2(元),
即:若通话时间为2分钟,该付费1.8元?若通话时间为10分钟,则该付10.2元
点评 本题考查了列代数式及求代数式的值的应用问题,解题的关键是审清题目所含的数量关系解出代数式.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
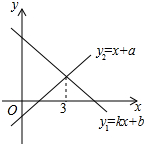 一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k>0;②a>0;③当x<3时,y1<y2中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论:①k>0;②a>0;③当x<3时,y1<y2中,正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com